A car is travelling on a straight road. The maximum velocity the car Can attain is 24ms−1. The maximum acceleration and deceleration it can attain are 1ms−2 and 4ms−2 respectively. The shortest time the car takes from rest to rest in a distance of 200 m is,
22.4s (b) 30 s (c) 11.2 s (d) 5.6 s
30s
11.2s
5.6s
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the car as it accelerates and decelerates.
Step 1: Understand the motion phases
The car starts from rest, accelerates to its maximum velocity, then decelerates back to rest. We denote:
- Maximum velocity Vmax=24m/s
- Maximum acceleration a=1m/s2
- Maximum deceleration b=4m/s2
Step 2: Determine the time taken to reach maximum velocity
Using the formula for acceleration:
V=u+at
where u=0 (initial velocity), we can find the time ta taken to reach maximum velocity:
24=0+1⋅ta⟹ta=24s
Step 3: Calculate the distance covered during acceleration
The distance sa covered during the acceleration phase can be calculated using:
s=ut+12at2
Substituting u=0:
sa=0+12⋅1⋅t2a=12⋅1⋅(24)2=288m
Step 4: Determine the time taken to decelerate
Since the car decelerates at b=4m/s2, the time td taken to come to rest from Vmax is:
0=24−4td⟹td=244=6s
Step 5: Calculate the distance covered during deceleration
Using the same formula for distance:
sd=Vmaxtd−12bt2d
Substituting the values:
sd=24⋅6−12⋅4⋅(6)2=144−72=72m
Step 6: Total distance and time
The total distance covered during both phases is:
stotal=sa+sd=288+72=360m
However, we need to cover only 200 m. Thus, we need to adjust the time spent accelerating and decelerating.
Step 7: Set up the equations for the total distance
Let t be the time spent accelerating. The distance covered during acceleration is:
sa=12⋅1⋅t2=t22
The time spent decelerating is t4 (as given in the problem). The distance during deceleration is:
sd=24⋅t4−12⋅4⋅(t4)2=6t−12⋅4⋅t216=6t−t28
Step 8: Total distance equation
Setting the total distance to 200 m:
t22+6t−t28=200
Multiplying through by 8 to eliminate the fraction:
4t2+48t−t2=1600
This simplifies to:
3t2+48t−1600=0
Step 9: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
t=−48±√482−4⋅3⋅(−1600)2⋅3
Calculating the discriminant:
t=−48±√2304+192006
t=−48±√215046
Calculating √21504≈146.6:
t=−48+146.66≈16.433s
Step 10: Total time for the journey
The total time taken is:
T=t+t4=t(1+14)=5t4≈5⋅16.4334≈20.54s
Final Answer
The shortest time the car takes from rest to rest in a distance of 200 m is approximately 20.54 seconds.
The car starts from rest, accelerates to its maximum velocity, then decelerates back to rest. We denote:
- Maximum velocity Vmax=24m/s
- Maximum acceleration a=1m/s2
- Maximum deceleration b=4m/s2
Using the formula for acceleration:
V=u+at
where u=0 (initial velocity), we can find the time ta taken to reach maximum velocity:
24=0+1⋅ta⟹ta=24s
The distance sa covered during the acceleration phase can be calculated using:
s=ut+12at2
Substituting u=0:
sa=0+12⋅1⋅t2a=12⋅1⋅(24)2=288m
Since the car decelerates at b=4m/s2, the time td taken to come to rest from Vmax is:
0=24−4td⟹td=244=6s
Using the same formula for distance:
sd=Vmaxtd−12bt2d
Substituting the values:
sd=24⋅6−12⋅4⋅(6)2=144−72=72m
The total distance covered during both phases is:
stotal=sa+sd=288+72=360m
However, we need to cover only 200 m. Thus, we need to adjust the time spent accelerating and decelerating.
Let t be the time spent accelerating. The distance covered during acceleration is:
sa=12⋅1⋅t2=t22
The time spent decelerating is t4 (as given in the problem). The distance during deceleration is:
sd=24⋅t4−12⋅4⋅(t4)2=6t−12⋅4⋅t216=6t−t28
Setting the total distance to 200 m:
t22+6t−t28=200
Multiplying through by 8 to eliminate the fraction:
4t2+48t−t2=1600
This simplifies to:
3t2+48t−1600=0
Using the quadratic formula t=−b±√b2−4ac2a:
t=−48±√482−4⋅3⋅(−1600)2⋅3
Calculating the discriminant:
t=−48±√2304+192006
t=−48±√215046
Calculating √21504≈146.6:
t=−48+146.66≈16.433s
The total time taken is:
T=t+t4=t(1+14)=5t4≈5⋅16.4334≈20.54s
The shortest time the car takes from rest to rest in a distance of 200 m is approximately 20.54 seconds.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A car is travelling on a road. The maximum velocity the car can attain is 24ms−1 and the maximum deceleration is 4ms−2. If car starts from rest and comes to rest after travelling 1032m in the shortest time of 56 s, the maximum acceleration that the car can attain is
View SolutionThe velocity-time graph of a body is given in. The maximum acceleration in ms−1 is .
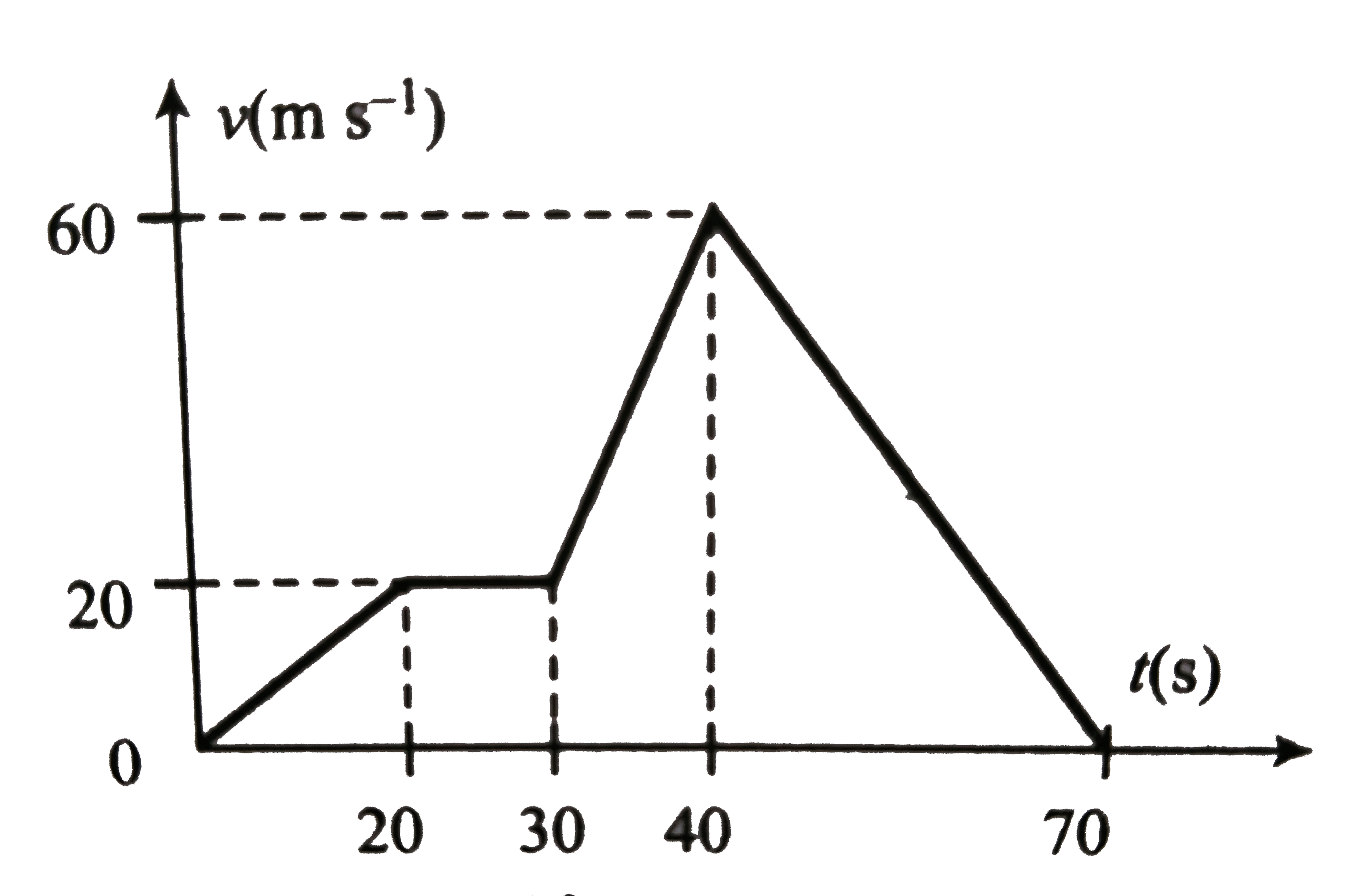 .
.
View SolutionThe maximum transverse velocity and maximum transverse acceleration of a harmonic wave in a one - dimensional string are 1ms−1and1ms−2 respectively. The phase velocity of the wave is 1ms−1. The waveform is
View SolutionThe minimum and maximum velocities of a projectile are 10ms−1 and 20ms−1 respectively. The horizontal range and maximum height are respectively (g=10 ms−2)
View SolutionA particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
View SolutionA car of mass m has an engine which can deliver constant power P.the maximum speed that the car can attain in t seconds in
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
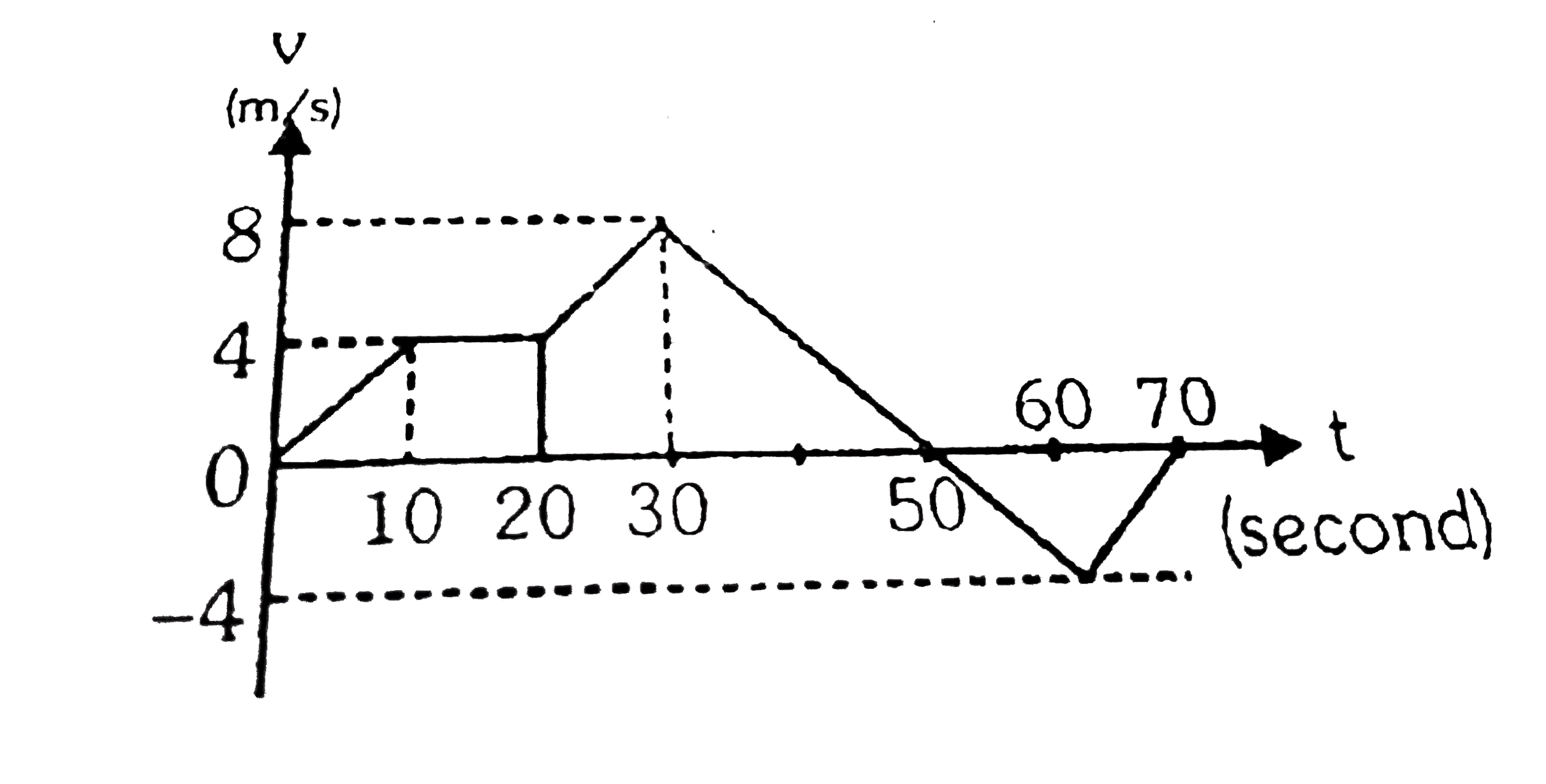
The maximum displacement from the starting position will be :-
View SolutionA car 2 m long travelling at 30ms−1 overtakes another car 4 m long travelling at 20ms−1. The time taken by the first car to pass the second car is
View SolutionA car is to be hoisted by elevator to the fourth floor of a parking garage, which is 14 m above the ground. If the elevator can have maximum acceleration of 0.2m/s2 and maximum deceleration of 0.1m/s2 and can reach a maximum speed of 2.5 m//s, determine the shortest time to make the lift, starting from rest and ending at rest.
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View Solution
