If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
The correct Answer is:B, C
To solve the problem, we need to determine the acceleration of a particle whose velocity decreases linearly with displacement. Here’s a step-by-step solution:
Step 1: Establish the relationship between velocity and displacement
The problem states that the velocity v decreases linearly from 20m/s at s=0 to 0m/s at s=30m. We can express this relationship as a linear equation:
v=mx+c
where m is the slope and c is the y-intercept.
Step 2: Determine the slope (m) and y-intercept (c)
From the given points:
- At s=0, v=20m/s (this gives us c=20)
- At s=30, v=0m/s
Using the two points to find the slope:
m=v2−v1s2−s1=0−2030−0=−2030=−23
Thus, the equation for velocity as a function of displacement s becomes:
v=−23s+20
Step 3: Find the velocity at s=15m
Now, we can calculate the velocity when s=15m:
v=−23(15)+20=−10+20=10m/s
Step 4: Find the derivative of velocity with respect to displacement
Next, we need to find dvds:
dvds=−23(constant)
Step 5: Calculate the acceleration using the formula
The acceleration a can be expressed in terms of velocity and its derivative:
a=vdvds
Substituting the values we have:
a=10(−23)=−203m/s2
Final Answer
Thus, the acceleration of the particle when s=15m is:
a=−203m/s2
---
The problem states that the velocity v decreases linearly from 20m/s at s=0 to 0m/s at s=30m. We can express this relationship as a linear equation:
v=mx+c
where m is the slope and c is the y-intercept.
From the given points:
- At s=0, v=20m/s (this gives us c=20)
- At s=30, v=0m/s
m=v2−v1s2−s1=0−2030−0=−2030=−23
Thus, the equation for velocity as a function of displacement s becomes:
v=−23s+20
Now, we can calculate the velocity when s=15m:
v=−23(15)+20=−10+20=10m/s
Next, we need to find dvds:
dvds=−23(constant)
The acceleration a can be expressed in terms of velocity and its derivative:
a=vdvds
Substituting the values we have:
a=10(−23)=−203m/s2
Thus, the acceleration of the particle when s=15m is:
a=−203m/s2
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Objective
Explore 45 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
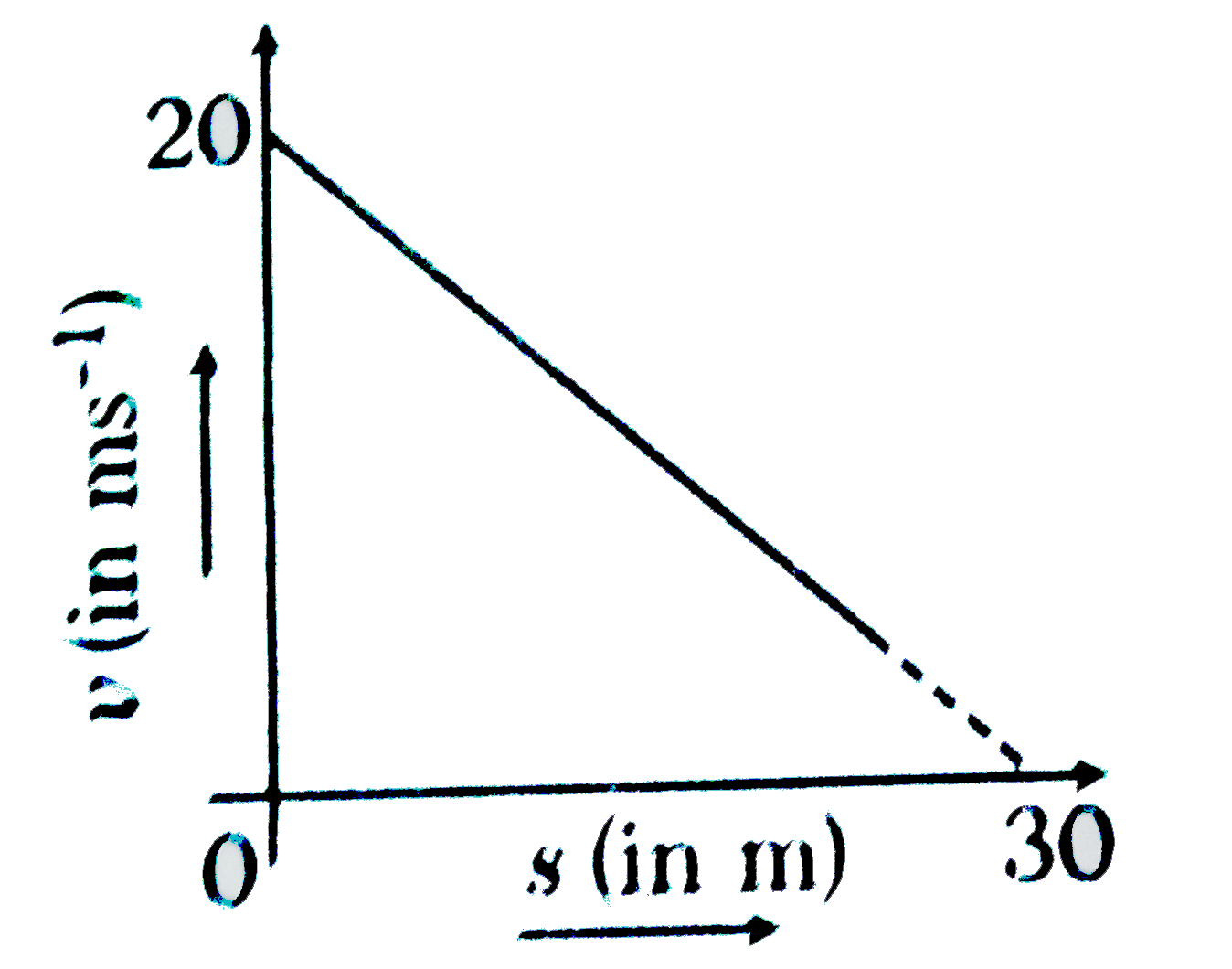
If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
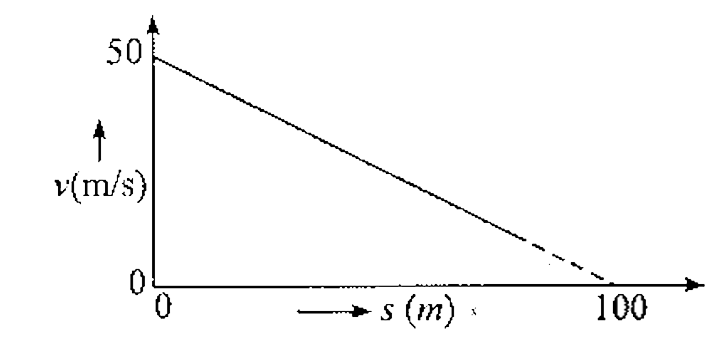
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its position coordinates s from 50m/s to a value approaching zero at = 100 m, the time it takes to reach the 100 m position will be:
View SolutionThe velocity of a particle moving in a straight line is decreasing at the rate of 3m/s per metre of displacement at an instant when the velocity is 10m/s. Determine the acceleration of the particle at this instant.
View SolutionIf the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionFind the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = log t and
View SolutionThe velocity-time graph of a particle moving along a straight line is shown in the figure-given below
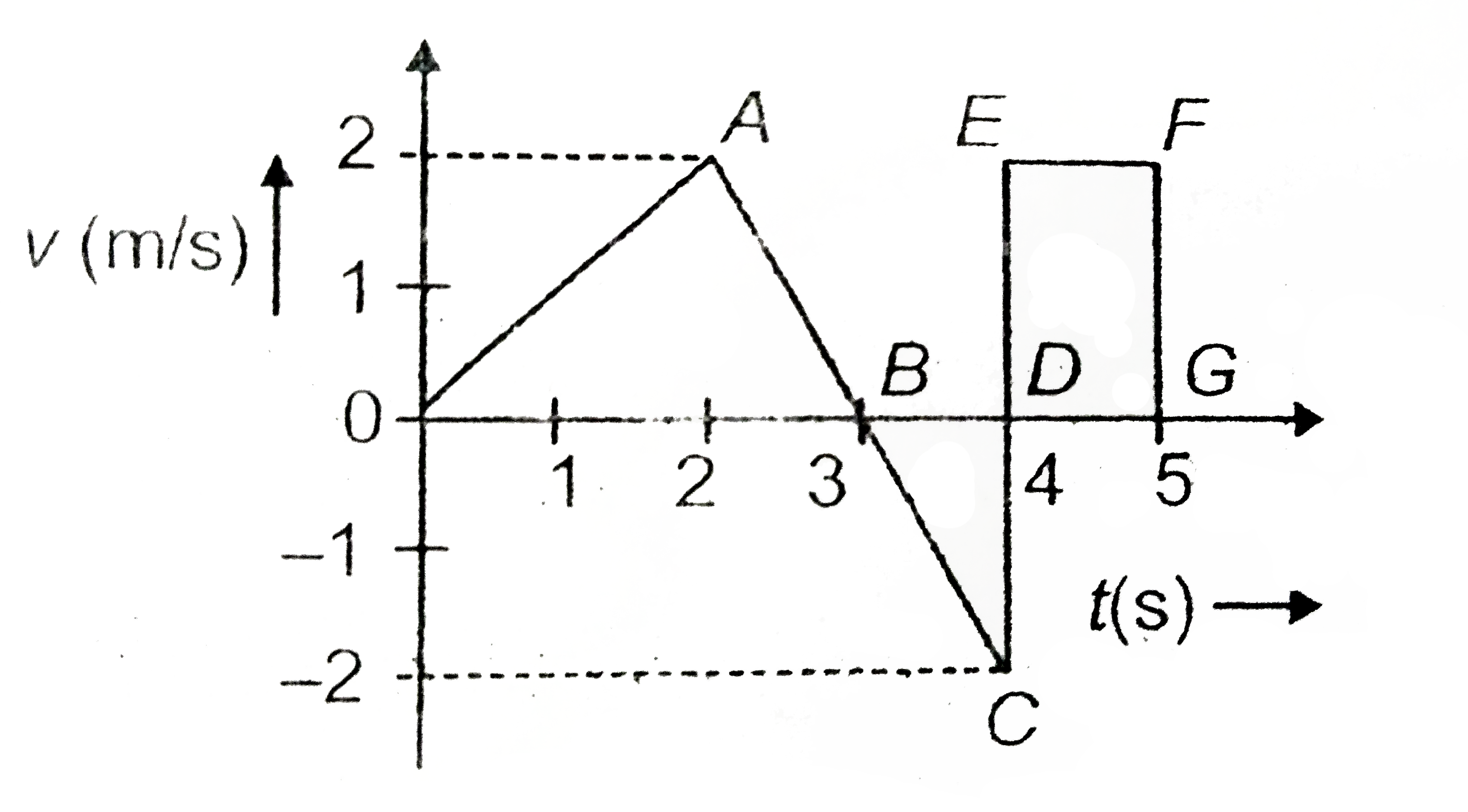
The displacement of the particle in 5 second is
0.5 m
1 m
2 m
4 m
View SolutionFind the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = sin (t/9)
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View Solution