A particle moves along a horizontal path, such that its velocity is given by v=(3t2−6t)m/s, where t is the time in seconds. If it is initially located at the origin O, determine the distance travelled by the particle in time interval from t=0 to t=3.5s and the particle's average velocity and average speed during the same time interval.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will follow these steps:
Step 1: Determine the velocity function
The velocity of the particle is given by:
v(t)=3t2−6tm/s
Step 2: Find the times when the velocity is zero
To find the time intervals where the particle changes direction, we set the velocity to zero:
3t2−6t=0
Factoring out 3t:
3t(t−2)=0
This gives us:
t=0ort=2s
Step 3: Analyze the velocity intervals
- For t<2s, the velocity is negative (the particle is moving in the negative direction).
- At t=2s, the velocity is zero (the particle momentarily stops).
- For t>2s, the velocity is positive (the particle moves in the positive direction).
Step 4: Calculate displacement from t=0 to t=3.5s
We need to break the calculation into two intervals: from t=0 to t=2 and from t=2 to t=3.5.
Interval 1: From t=0 to t=2
The displacement s1 is given by integrating the velocity:
s1=∫20(3t2−6t)dt
Calculating the integral:
s1=(t3−3t2)20=(23−3⋅22)−(0−0)=8−12=−4m
Interval 2: From t=2 to t=3.5
Now we calculate the displacement s2:
s2=∫3.52(3t2−6t)dt
Calculating the integral:
s2=(t3−3t2)3.52=((3.5)3−3(3.5)2)−(23−3(22))
Calculating each part:
(3.5)3=42.875,3(3.5)2=36.75
So,
s2=(42.875−36.75)−(−4)=6.125+4=10.125m
Step 5: Total displacement
The total displacement from t=0 to t=3.5 is:
Total displacement=s1+s2=−4+10.125=6.125m
Step 6: Calculate total distance travelled
The total distance travelled is the sum of the absolute values of the displacements:
Total distance=|s1|+|s2|=4+10.125=14.125m
Step 7: Calculate average velocity
The average velocity is given by:
Average velocity=Total displacementTotal time=6.1253.5≈1.75m/s
Step 8: Calculate average speed
The average speed is given by:
Average speed=Total distanceTotal time=14.1253.5≈4.03m/s
Final Answers
- Distance travelled: 14.125m
- Average velocity: 1.75m/s
- Average speed: 4.03m/s
The velocity of the particle is given by:
v(t)=3t2−6tm/s
To find the time intervals where the particle changes direction, we set the velocity to zero:
3t2−6t=0
Factoring out 3t:
3t(t−2)=0
This gives us:
t=0ort=2s
- For t<2s, the velocity is negative (the particle is moving in the negative direction).
- At t=2s, the velocity is zero (the particle momentarily stops).
- For t>2s, the velocity is positive (the particle moves in the positive direction).
We need to break the calculation into two intervals: from t=0 to t=2 and from t=2 to t=3.5.
The displacement s1 is given by integrating the velocity:
s1=∫20(3t2−6t)dt
Calculating the integral:
s1=(t3−3t2)20=(23−3⋅22)−(0−0)=8−12=−4m
Now we calculate the displacement s2:
s2=∫3.52(3t2−6t)dt
Calculating the integral:
s2=(t3−3t2)3.52=((3.5)3−3(3.5)2)−(23−3(22))
Calculating each part:
(3.5)3=42.875,3(3.5)2=36.75
So,
s2=(42.875−36.75)−(−4)=6.125+4=10.125m
The total displacement from t=0 to t=3.5 is:
Total displacement=s1+s2=−4+10.125=6.125m
The total distance travelled is the sum of the absolute values of the displacements:
Total distance=|s1|+|s2|=4+10.125=14.125m
The average velocity is given by:
Average velocity=Total displacementTotal time=6.1253.5≈1.75m/s
The average speed is given by:
Average speed=Total distanceTotal time=14.1253.5≈4.03m/s
- Distance travelled: 14.125m
- Average velocity: 1.75m/s
- Average speed: 4.03m/s
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Objective
Explore 45 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
The velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
View SolutionThe velocity of a particle is given by v=(4t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=1 second.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t=0 to t=14s, find
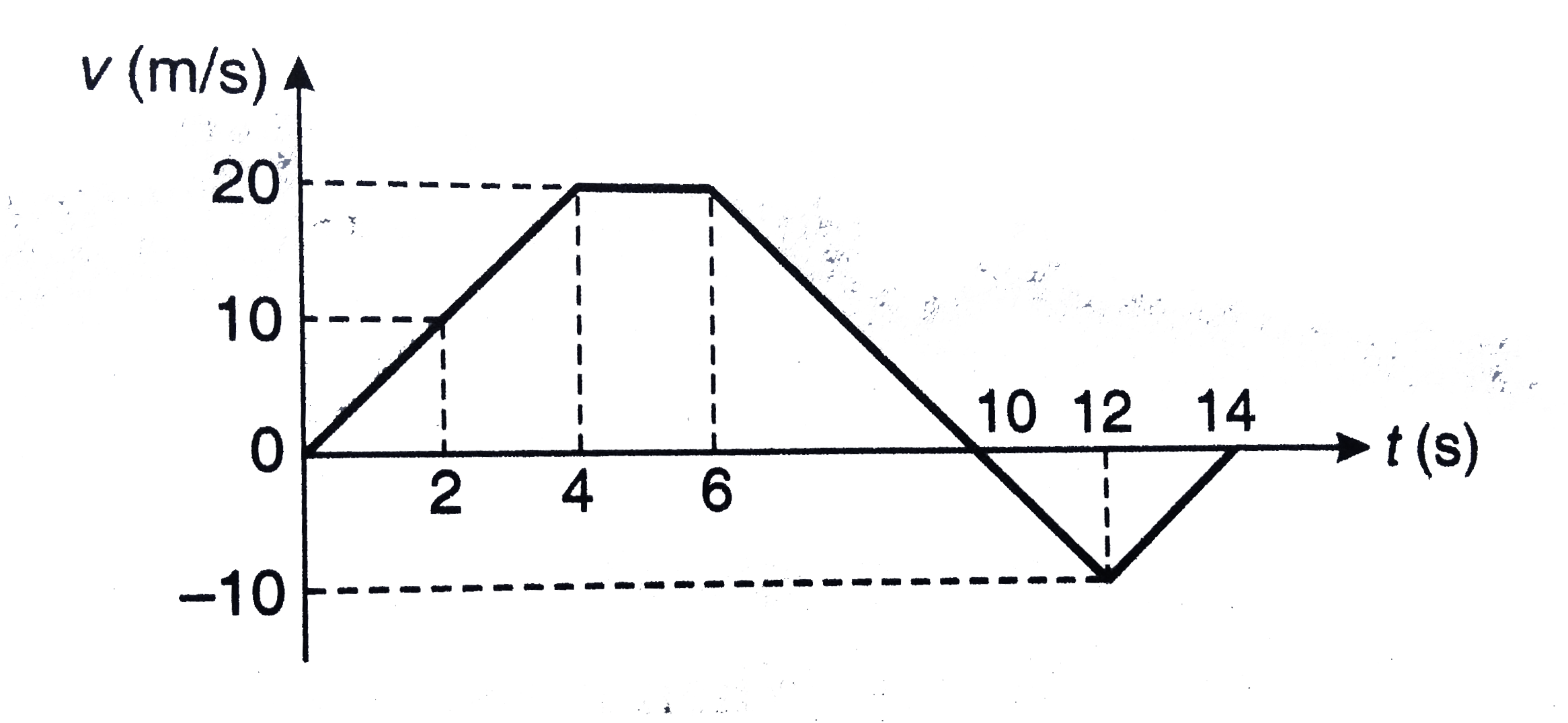
(a) average velocity and
(b) average speed of the particle.
View SolutionThe speed verses time graph for a particle is shown in the figure. The distance travelled (in m) by the particle during the time interval t = 0 to t = 5 s will be __________

View SolutionThe diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is

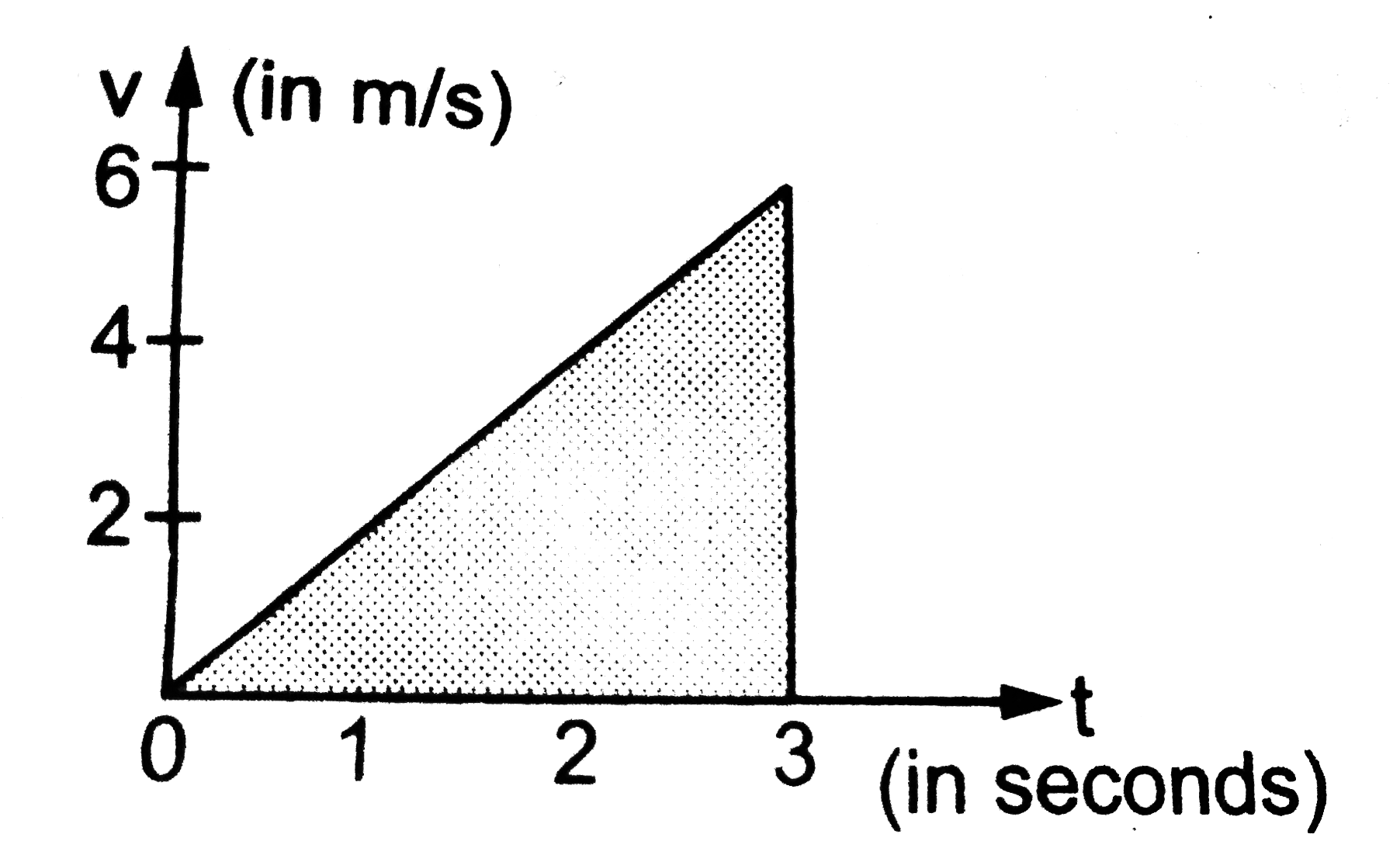
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
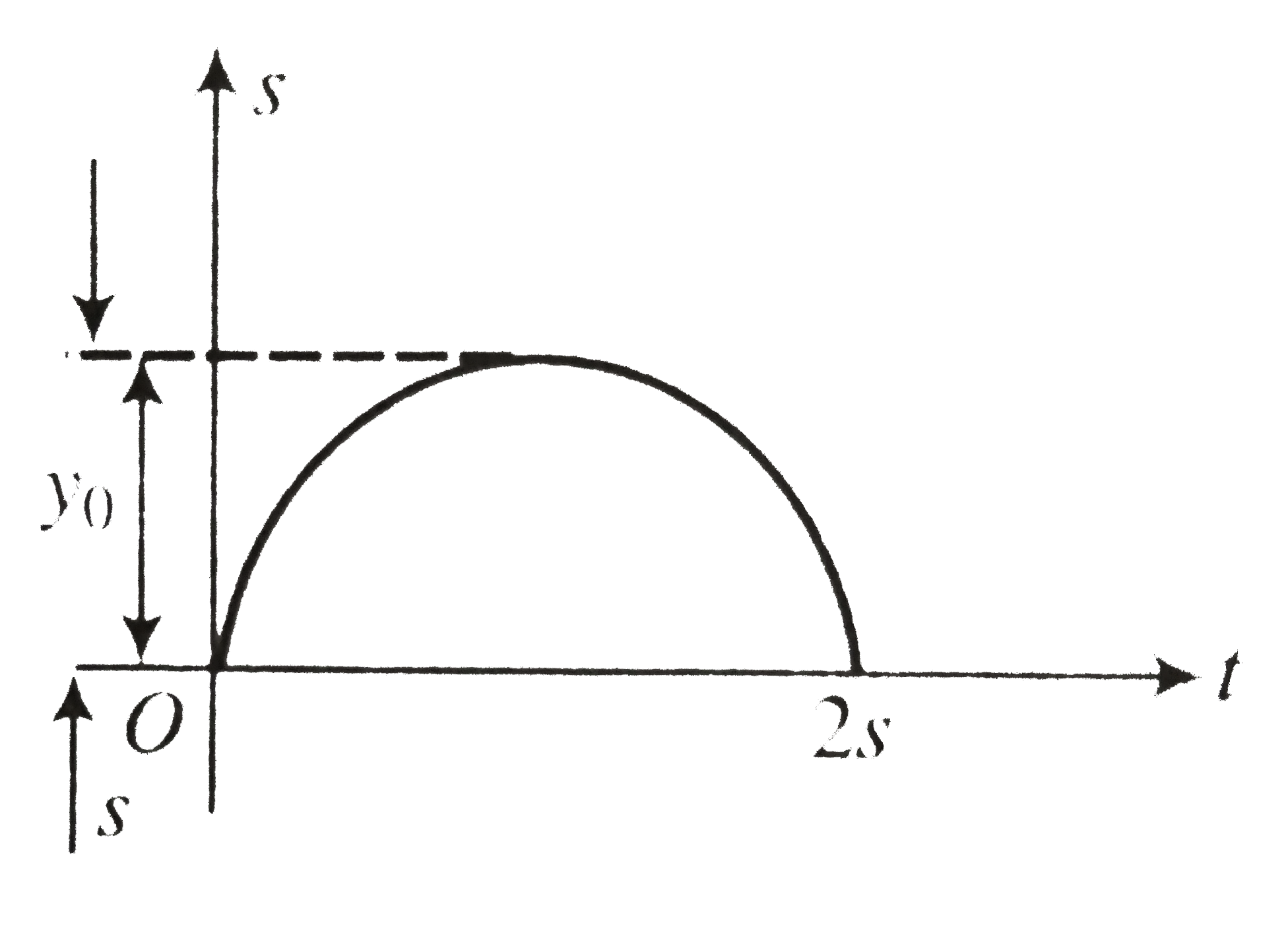
View SolutionA particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
View SolutionThe acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
View Solution