At time t=0, a particle is at (2m,4m). It starts moving towards positive x-axis with constant acceleration 2m/s2 (initial velocity=0). After 2 s, an additional acceleration of 4m/s2 starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.
The correct Answer is:A, B, D
To solve the problem step by step, we will break it down into two main parts: the first 2 seconds of motion and the next 2 seconds after the additional acceleration starts acting.
Step 1: Calculate the position and velocity after the first 2 seconds
1. Initial Conditions:
- Initial position r0=(2m,4m)
- Initial velocity u=0
- Acceleration in the x-direction a1=2m/s2
- Time t1=2s
2. Calculate the velocity in the x-direction after 2 seconds:
v1=u+a1t1=0+2×2=4m/s(in the x-direction)
3. Calculate the position in the x-direction after 2 seconds:
r1=r0+ut+12a1t21
r1=(2m,4m)+(0)+12×2×(22)=(2+4,4)=(6m,4m)
Step 2: Calculate the position and velocity after the next 2 seconds with additional acceleration
1. New Conditions:
- After 2 seconds, an additional acceleration a2=−4m/s2 (in the negative y-direction) starts acting.
- Time for this phase t2=2s
2. Calculate the velocity after the additional acceleration starts acting:
v2=v1+a2t2
Here, a2 has components: 2m/s2 in the x-direction and −4m/s2 in the y-direction.
v2=(4i)+(2i−4j)×2
v2=(4+4)i+(−8)j=8i−8jm/s
3. Calculate the new position after the additional acceleration:
r2=r1+v1t2+12a2t22
r2=(6m,4m)+(4m/s×2s)+12(2i−4j)×(22)
r2=(6,4)+(8,0)+(2×2,−4×2)=(6+8+8,4−8)=(22m,−4m)
Final Results:
- Velocity after 4 seconds: v2=8i−8jm/s
- Coordinates after 4 seconds: (22m,−4m)
- Initial position r0=(2m,4m)
- Initial velocity u=0
- Acceleration in the x-direction a1=2m/s2
- Time t1=2s
v1=u+a1t1=0+2×2=4m/s(in the x-direction)
r1=r0+ut+12a1t21
r1=(2m,4m)+(0)+12×2×(22)=(2+4,4)=(6m,4m)
- After 2 seconds, an additional acceleration a2=−4m/s2 (in the negative y-direction) starts acting.
- Time for this phase t2=2s
v2=v1+a2t2
Here, a2 has components: 2m/s2 in the x-direction and −4m/s2 in the y-direction.
v2=(4i)+(2i−4j)×2
v2=(4+4)i+(−8)j=8i−8jm/s
r2=r1+v1t2+12a2t22
r2=(6m,4m)+(4m/s×2s)+12(2i−4j)×(22)
r2=(6,4)+(8,0)+(2×2,−4×2)=(6+8+8,4−8)=(22m,−4m)
- Velocity after 4 seconds: v2=8i−8jm/s
- Coordinates after 4 seconds: (22m,−4m)
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
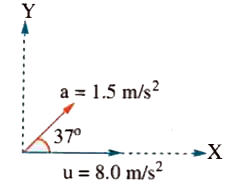
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle of mass 2kg starts moving in a straight line with an initial velocity of 2m/s at a constant acceleration of 2m/s2. Then rate of change of kinetic energy.
View SolutionVelocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View Solution
