Two bodies are projected vertically upwards from one point with the same initial velocity v0. The second body is projected t0s after the first. How long after will the bodies meet?
The correct Answer is:B
To solve the problem of when the two bodies meet after being projected vertically upwards, we can follow these steps:
Step 1: Understand the motion of both bodies
Let:
- Body 1 is projected at time t=0 with initial velocity v0.
- Body 2 is projected at time t=t0 with the same initial velocity v0.
Step 2: Write the displacement equations
Using the equation of motion for both bodies, we can express their displacements:
For Body 1 (projected at t=0):
s1=v0t−12gt2
For Body 2 (projected at t=t0):
Since Body 2 is projected t0 seconds after Body 1, its time of flight when the collision occurs will be t−t0:
s2=v0(t−t0)−12g(t−t0)2
Step 3: Set the displacements equal
At the time of collision, the displacements of both bodies will be equal:
s1=s2
Substituting the expressions for s1 and s2:
v0t−12gt2=v0(t−t0)−12g(t−t0)2
Step 4: Simplify the equation
Expanding the right side:
v0t−12gt2=v0t−v0t0−12g(t2−2tt0+t20)
Now, simplifying both sides:
v0t−12gt2=v0t−v0t0−12gt2+gtt0−12gt20
Step 5: Cancel common terms
Cancelling v0t and −12gt2 from both sides:
0=−v0t0+gtt0−12gt20
Step 6: Rearranging the equation
Rearranging gives:
gtt0=v0t0+12gt20
Dividing both sides by t0 (assuming t0≠0):
gt=v0+12gt0
Step 7: Solve for t
Now, solving for t:
t=v0g+12t0
Final Answer
Thus, the time after which the two bodies will meet is:
t=v0g+12t0
---
Let:
- Body 1 is projected at time t=0 with initial velocity v0.
- Body 2 is projected at time t=t0 with the same initial velocity v0.
Using the equation of motion for both bodies, we can express their displacements:
s1=v0t−12gt2
Since Body 2 is projected t0 seconds after Body 1, its time of flight when the collision occurs will be t−t0:
s2=v0(t−t0)−12g(t−t0)2
At the time of collision, the displacements of both bodies will be equal:
s1=s2
Substituting the expressions for s1 and s2:
v0t−12gt2=v0(t−t0)−12g(t−t0)2
Expanding the right side:
v0t−12gt2=v0t−v0t0−12g(t2−2tt0+t20)
Now, simplifying both sides:
v0t−12gt2=v0t−v0t0−12gt2+gtt0−12gt20
Cancelling v0t and −12gt2 from both sides:
0=−v0t0+gtt0−12gt20
Rearranging gives:
gtt0=v0t0+12gt20
Dividing both sides by t0 (assuming t0≠0):
gt=v0+12gt0
Now, solving for t:
t=v0g+12t0
Thus, the time after which the two bodies will meet is:
t=v0g+12t0
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Subjective
Explore 50 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Assertion And Reason
Explore 12 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
View SolutionTwo bodies are thrown verically upward, with the same initially velocity of 98m/s, but the second one is thrown 4 sec. after first is thrown. If after 4n seconds after the first particle is thrown, both of them meet then value of n is ?
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View SolutionVelocity-time curve for a body projected vertically upwards is with times (s)
View SolutionA body is projected vertically upward with an initial velocity u. If acceleration due to gravity is g, find the time for which it remains in air.
View SolutionA body is thrown vertically up with a velocity of 100 m/s and another one is thrown 4 sec after the first one. How long after the first one is thrown will they meet?
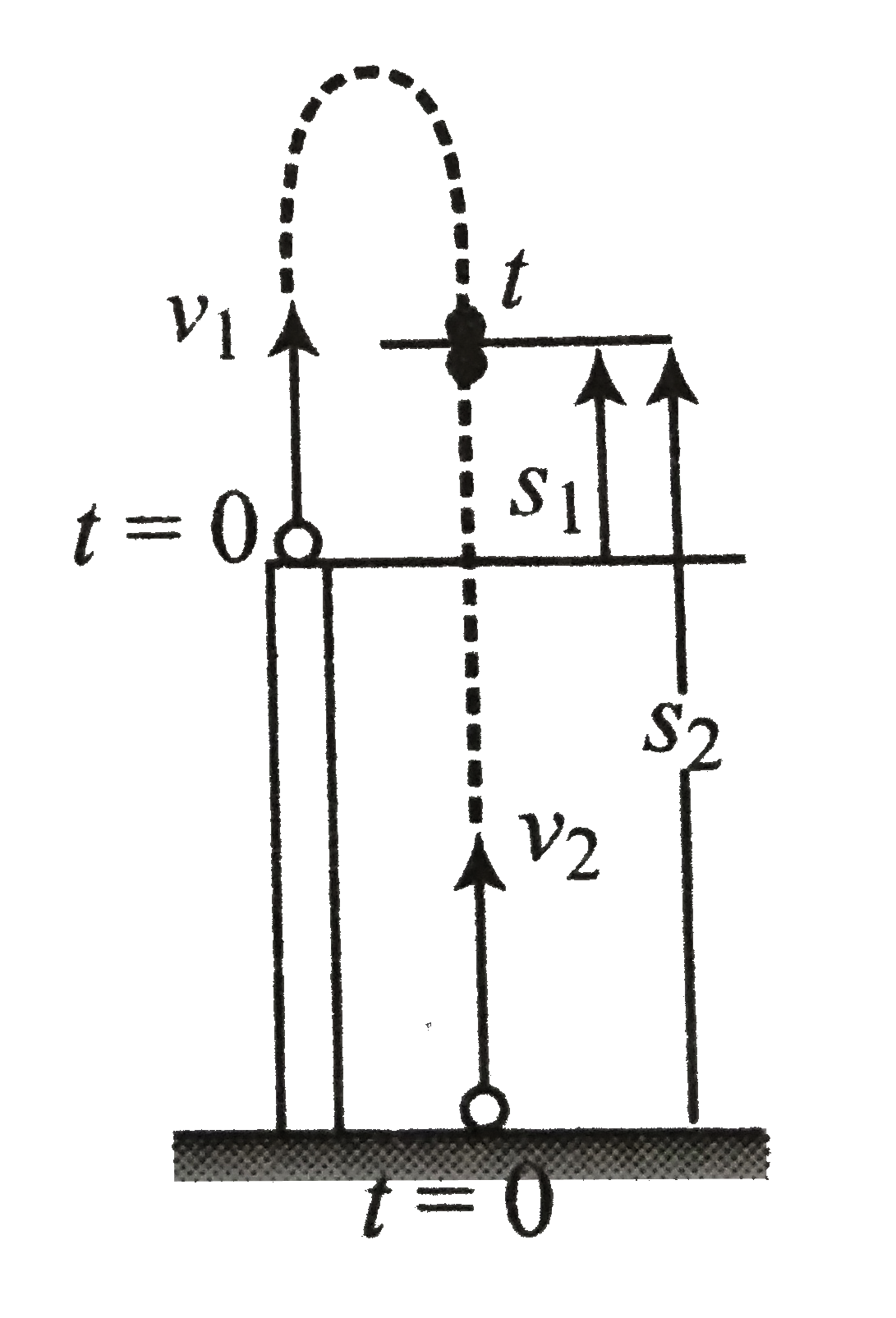
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
View SolutionThere are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View SolutionA particlele is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particel with the same speed v at an angle of projection θ with the horizontal in upwards direction. The time when the distance between them is minimum is
View SolutionTwo bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
View Solution

