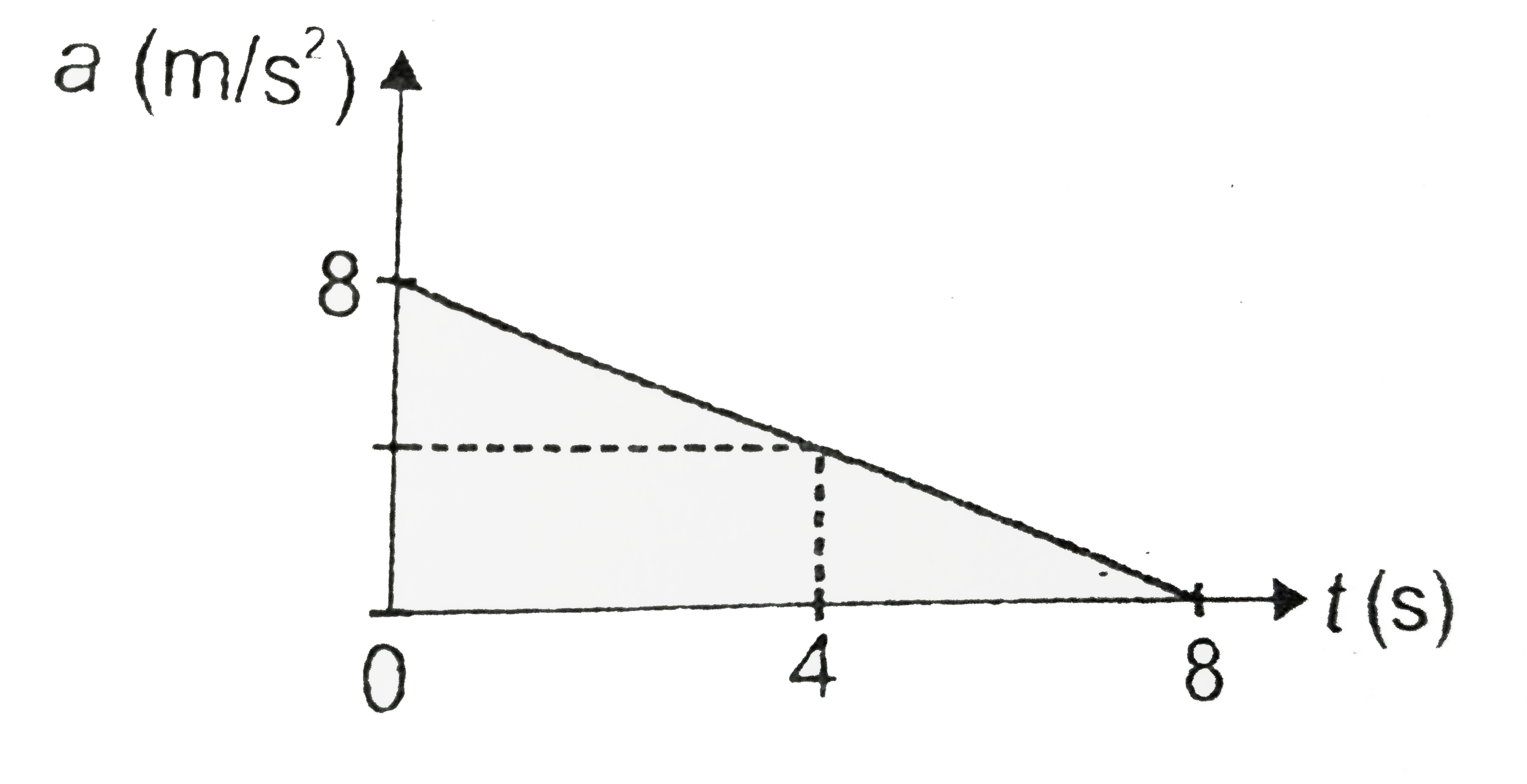
The graph describes an airplane's acceleration during its take-off run. The airplane's velocity when it lifts oof at t=20s is
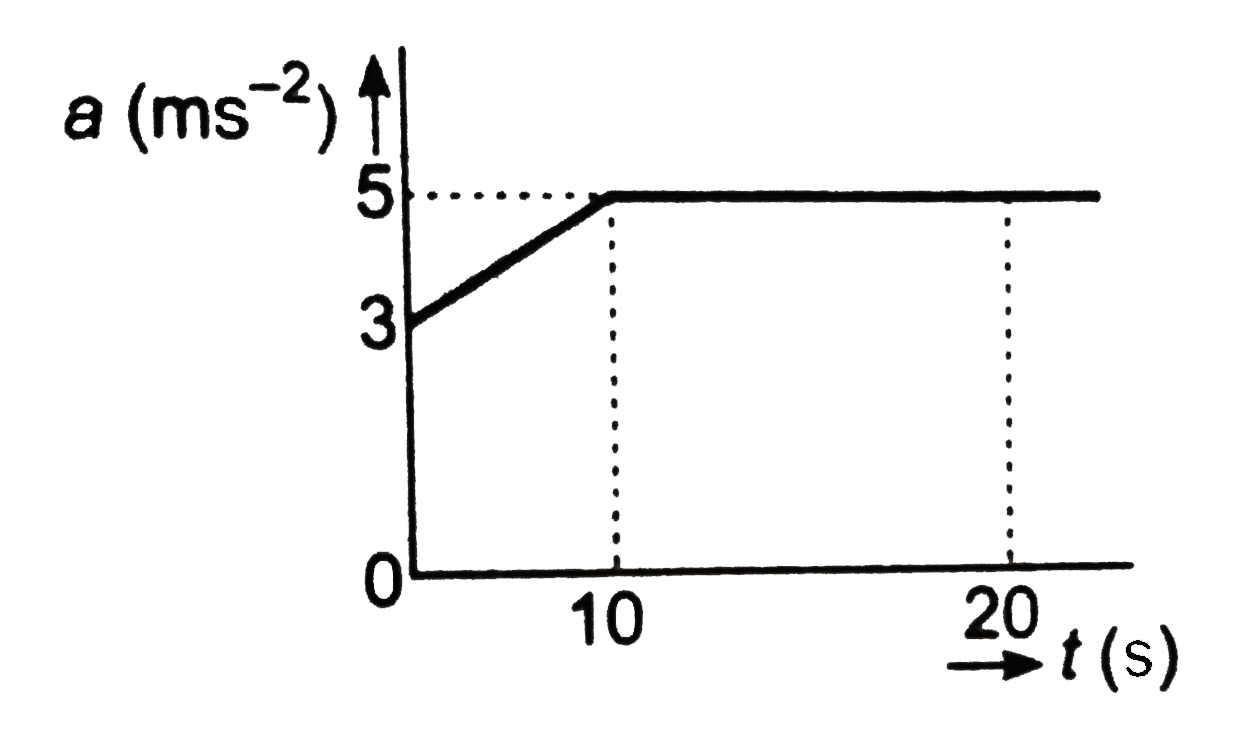
40ms−1
50ms−1
90ms−1
180ms−1
The correct Answer is:B
Δv=vf−vi=area under a-t graph
vi=0
⇒vf=area
=40+50
=90m/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective50videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Assertion And Reason12videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
The v-s graph for an airplane travelling on a straight runway is shown. Determine the acceleration of the plane at s=50m and s=150m. Draw the a-s graph.
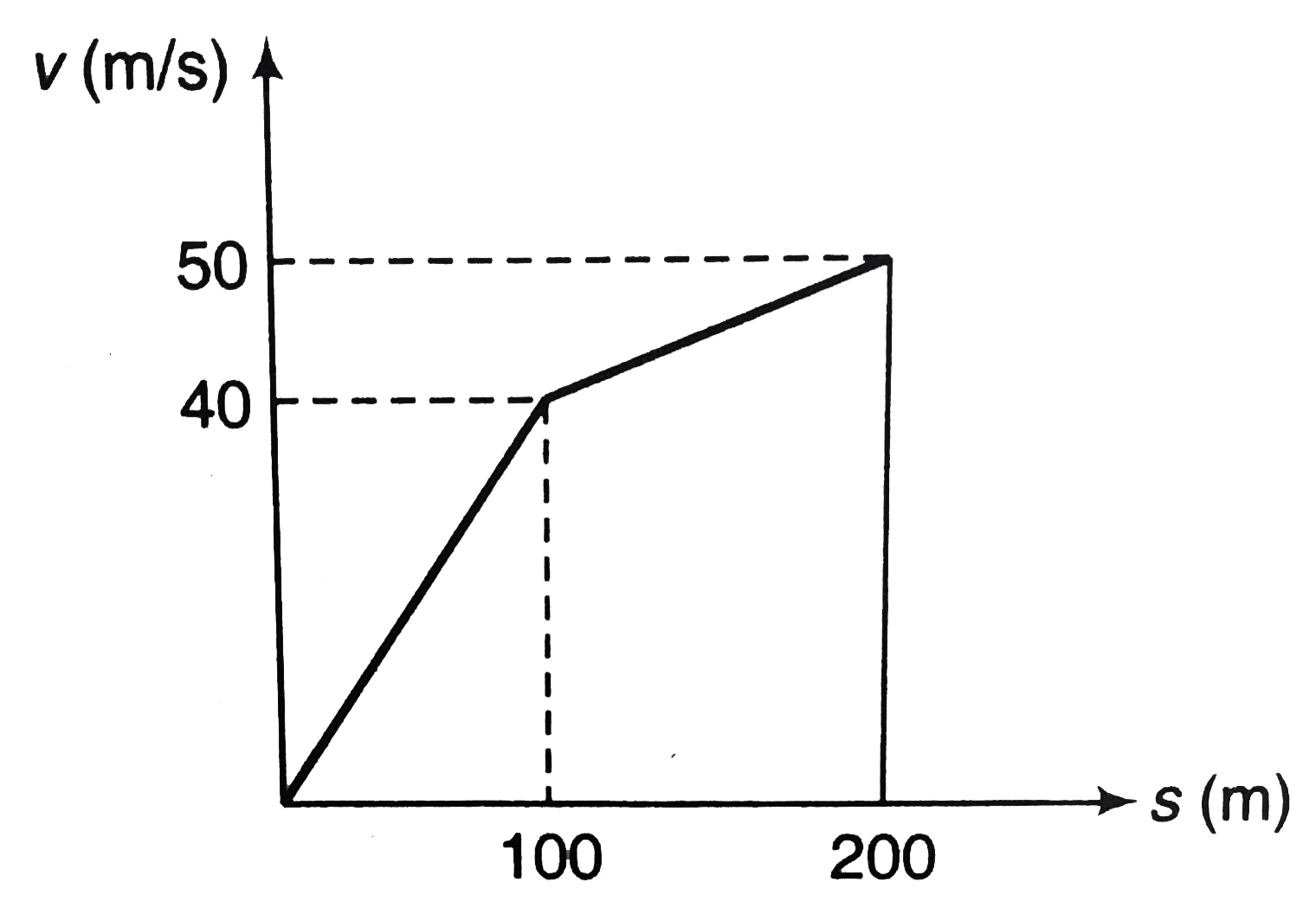 View Solution
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope will change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
For the given velocity-time graph the displacement of the object between t = 2 s to t = 4 s is
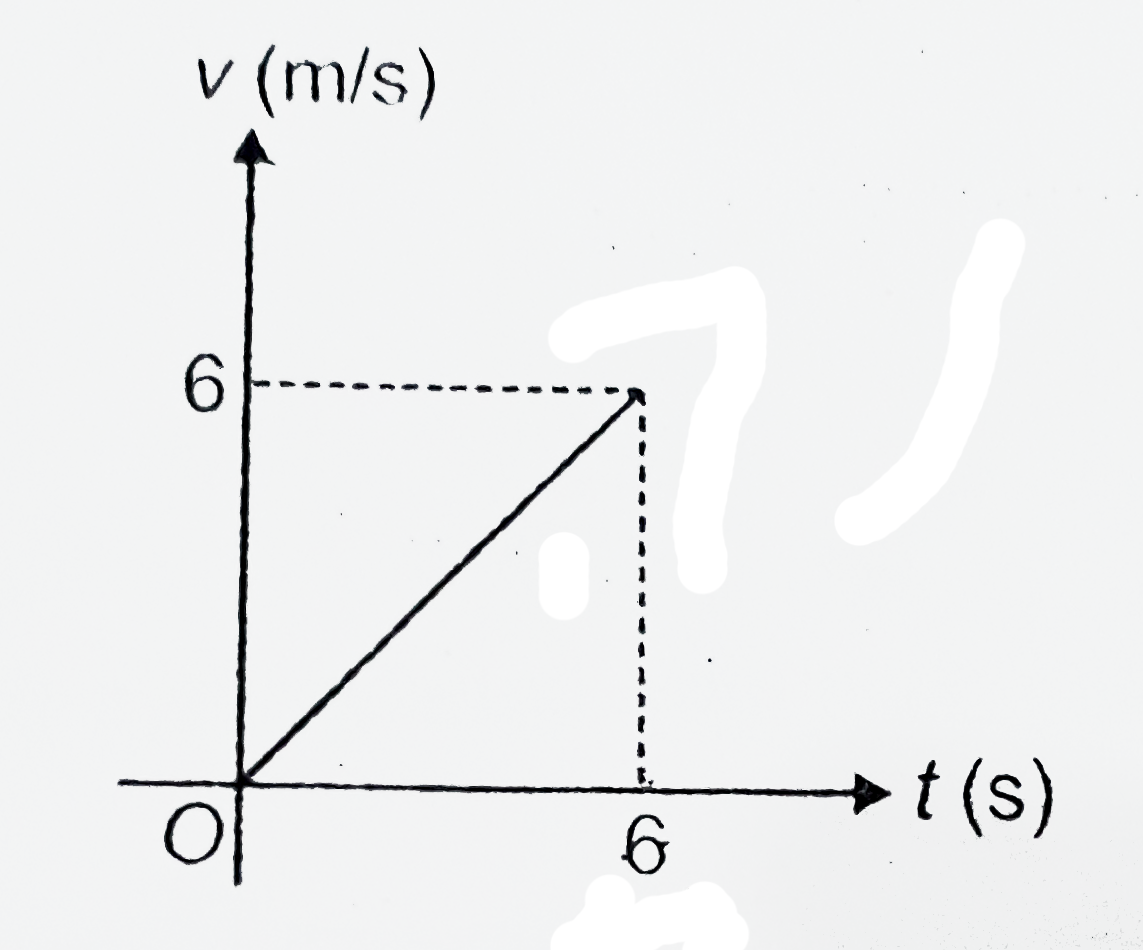 View Solution
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
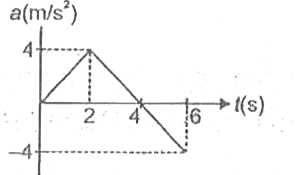 View Solution
View SolutionAn aeroplane of mass 10,000 kg requires a speed of 20 ms−1 for take-off run of 100 m on the ground. The coefficient of kinetic friction between the wheels of the plane and ground is 0.3. Assume that the plane accelerates uniformly during the take off. Determine the minimum force required by the engine of the plane to take off (g=10ms−2).
View SolutionAn aeroplane requires a speed of 72 kmph for a take off with 150m run on the ground. The mass of the plane is 1500kg and the coefficient of friction between the aeroplane and the ground is 0.4. Assuming that the aeroplane acceleration uniformly during take off, find the minimum force exerted by the engine of the aeroplane for take off.
View SolutionA particle moving with uniform acceleration passes the point x=2m with velocity 20m/s at the instant t=0. Some time later it is observed at the point x=32m moving with velocity 10m/s.
(a) What is its acceleration?
(b) Find its position nd velocity at the instant t=8s.
(c) What is the distance traveled during the interval t=0 to 8s?View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.
View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and t = 1 s.View SolutionFind the average acceleration in first 20s. (Hint: Area under a−t graph is equal to the change in velocity).
 .View Solution
.View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View Solution
