An aeroplane of mass 10,000 kg requires a speed of 20 ms−1 for take-off run of 100 m on the ground. The coefficient of kinetic friction between the wheels of the plane and ground is 0.3. Assume that the plane accelerates uniformly during the take off. Determine the minimum force required by the engine of the plane to take off (g=10ms−2).
To solve the problem, we will follow these steps:
Step 1: Identify the given data
- Mass of the aeroplane, m=10,000kg
- Final speed required for take-off, v=20m/s
- Distance for take-off run, s=100m
- Coefficient of kinetic friction, μ=0.3
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the required acceleration
We can use the kinematic equation:
v2=u2+2as
where:
- u=0m/s (initial speed)
- v=20m/s (final speed)
- s=100m (distance)
Substituting the values:
(20)2=(0)2+2a(100)
400=200a
a=400200=2m/s2
Step 3: Calculate the maximum acceleration due to friction
The maximum acceleration that can be provided by friction is given by:
afriction=μg
Substituting the values:
afriction=0.3×10=3m/s2
Step 4: Check if friction can provide the required acceleration
Since the required acceleration a=2m/s2 is less than the maximum frictional acceleration afriction=3m/s2, the friction is sufficient.
Step 5: Calculate the minimum force required by the engine
The net force required to achieve the acceleration can be calculated using Newton's second law:
Fnet=ma
Substituting the values:
Fnet=10,000×2=20,000N
Step 6: Consider the force of friction
The force of friction Ffriction acting against the motion can be calculated as:
Ffriction=μmg=0.3×10,000×10=30,000N
Step 7: Calculate the total force required by the engine
The total force required by the engine Fengine must overcome the frictional force and provide the net force:
Fengine=Fnet+Ffriction=20,000+30,000=50,000N
Final Answer
The minimum force required by the engine of the plane to take off is:
50,000N
---
- Mass of the aeroplane, m=10,000kg
- Final speed required for take-off, v=20m/s
- Distance for take-off run, s=100m
- Coefficient of kinetic friction, μ=0.3
- Acceleration due to gravity, g=10m/s2
We can use the kinematic equation:
v2=u2+2as
where:
- u=0m/s (initial speed)
- v=20m/s (final speed)
- s=100m (distance)
(20)2=(0)2+2a(100)
400=200a
a=400200=2m/s2
The maximum acceleration that can be provided by friction is given by:
afriction=μg
Substituting the values:
afriction=0.3×10=3m/s2
Since the required acceleration a=2m/s2 is less than the maximum frictional acceleration afriction=3m/s2, the friction is sufficient.
The net force required to achieve the acceleration can be calculated using Newton's second law:
Fnet=ma
Substituting the values:
Fnet=10,000×2=20,000N
The force of friction Ffriction acting against the motion can be calculated as:
Ffriction=μmg=0.3×10,000×10=30,000N
The total force required by the engine Fengine must overcome the frictional force and provide the net force:
Fengine=Fnet+Ffriction=20,000+30,000=50,000N
The minimum force required by the engine of the plane to take off is:
50,000N
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 01BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECTION - C (Answer the following )
9 Videos
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D
6 Videos
- SELF ASSESSMENT PAPER 02BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-D (Answer the following )
6 Videos
Similar Questions
An aeroplane requires a speed of 72 kmph for a take off with 150m run on the ground. The mass of the plane is 1500kg and the coefficient of friction between the aeroplane and the ground is 0.4. Assuming that the aeroplane acceleration uniformly during take off, find the minimum force exerted by the engine of the aeroplane for take off.
View SolutionFind the force required to pull a block of mass 100kg up an incline of 8∘ at a uniform speed of 5m/s. The coefficient of friction between the block and the plane is 0.3.
View Solution
Knowledge Check
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g=10ms−2)
A2ms−2B4ms−2C6ms−2D8ms−2The coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
A√15ms−1B√3ms−1C√30ms−1D√10ms−1
Find the value of friction forces between the blocks A and B and between B and ground. ( Take , g=10ms−2)

View SolutionFind the maximum speed at which a car can take turn round a curve of 30 cm radius on a level road if the coefficient of friction between the tyres and the road is 0.4. Take g=10ms−2.
View SolutionThe coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30° with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. Find the least force required to pull the body up the plane.
View SolutionWhat is the acceleration of the block and trolley system shown in if the coefficient of kinetic friction between the trolley and the surface is 0 .04 ? What is the tension in the string ? Take g=10ms−2 Neglect the mass of the string
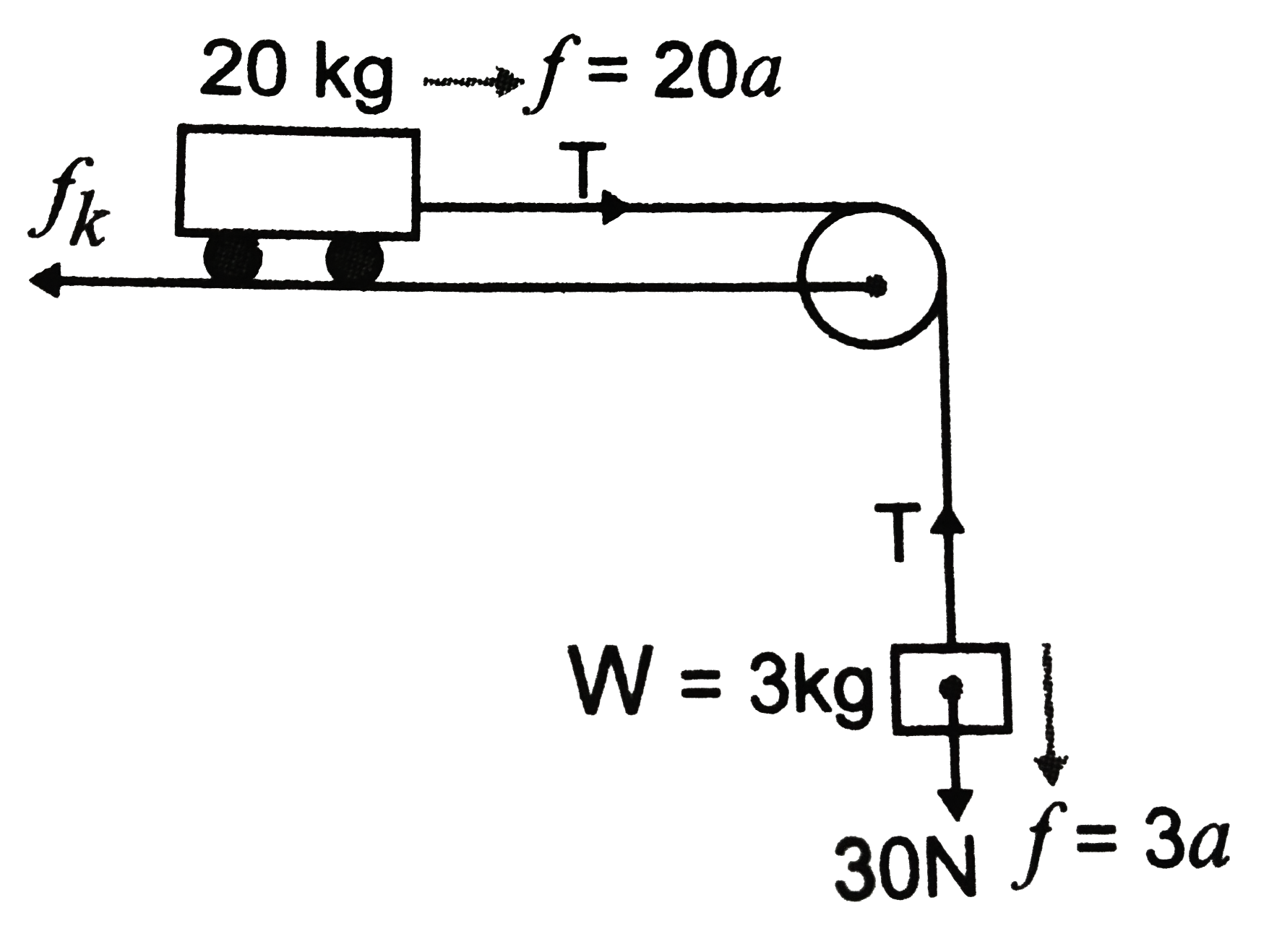 .
.
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View Solution
