Two trains are moving with velocities v1=10ms−1andv2=20ms−1 on the same track in opposite directions. After the application of brakes if their retarding rates are a1=2ms−2anda2=1ms−2 respectively, then the minimum distance of separation between the trains to avoid collision is
150 m
225 m
450 m
300 m
The correct Answer is:B
To find the minimum distance of separation between two trains moving towards each other to avoid a collision, we can follow these steps:
Step 1: Identify the Given Values
- Velocity of Train 1, v1=10m/s
- Velocity of Train 2, v2=20m/s
- Retardation of Train 1, a1=2m/s2
- Retardation of Train 2, a2=1m/s2
Step 2: Use the Kinematic Equation
We need to find the distance each train travels before coming to a stop. We can use the kinematic equation:
v2=u2+2as
where:
- v is the final velocity (0 m/s, since the trains come to a stop),
- u is the initial velocity,
- a is the acceleration (negative for retardation),
- s is the distance traveled.
Step 3: Calculate the Stopping Distance for Train 1
For Train 1:
- Initial velocity, u1=10m/s
- Final velocity, v1=0m/s
- Retardation, a1=−2m/s2
Using the equation:
0=(10)2+2(−2)s1
Rearranging gives:
s1=1022×2=1004=25m
Step 4: Calculate the Stopping Distance for Train 2
For Train 2:
- Initial velocity, u2=20m/s
- Final velocity, v2=0m/s
- Retardation, a2=−1m/s2
Using the equation:
0=(20)2+2(−1)s2
Rearranging gives:
s2=2022×1=4002=200m
Step 5: Calculate the Minimum Distance of Separation
The minimum distance of separation d to avoid collision is the sum of the distances traveled by both trains:
d=s1+s2=25m+200m=225m
Final Answer
The minimum distance of separation between the trains to avoid collision is 225m.
---
- Velocity of Train 1, v1=10m/s
- Velocity of Train 2, v2=20m/s
- Retardation of Train 1, a1=2m/s2
- Retardation of Train 2, a2=1m/s2
We need to find the distance each train travels before coming to a stop. We can use the kinematic equation:
v2=u2+2as
where:
- v is the final velocity (0 m/s, since the trains come to a stop),
- u is the initial velocity,
- a is the acceleration (negative for retardation),
- s is the distance traveled.
For Train 1:
- Initial velocity, u1=10m/s
- Final velocity, v1=0m/s
- Retardation, a1=−2m/s2
0=(10)2+2(−2)s1
Rearranging gives:
s1=1022×2=1004=25m
For Train 2:
- Initial velocity, u2=20m/s
- Final velocity, v2=0m/s
- Retardation, a2=−1m/s2
0=(20)2+2(−1)s2
Rearranging gives:
s2=2022×1=4002=200m
The minimum distance of separation d to avoid collision is the sum of the distances traveled by both trains:
d=s1+s2=25m+200m=225m
The minimum distance of separation between the trains to avoid collision is 225m.
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Subjective
Explore 50 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Assertion And Reason
Explore 12 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
The driver of a train moving at 72kmh−1 sights another train moving at 4ms−1 on the same track and in the same direction. He instantly applies brakes to produces a retardation of 1ms−2. The minimum distance between the trains so that no collision occurs is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
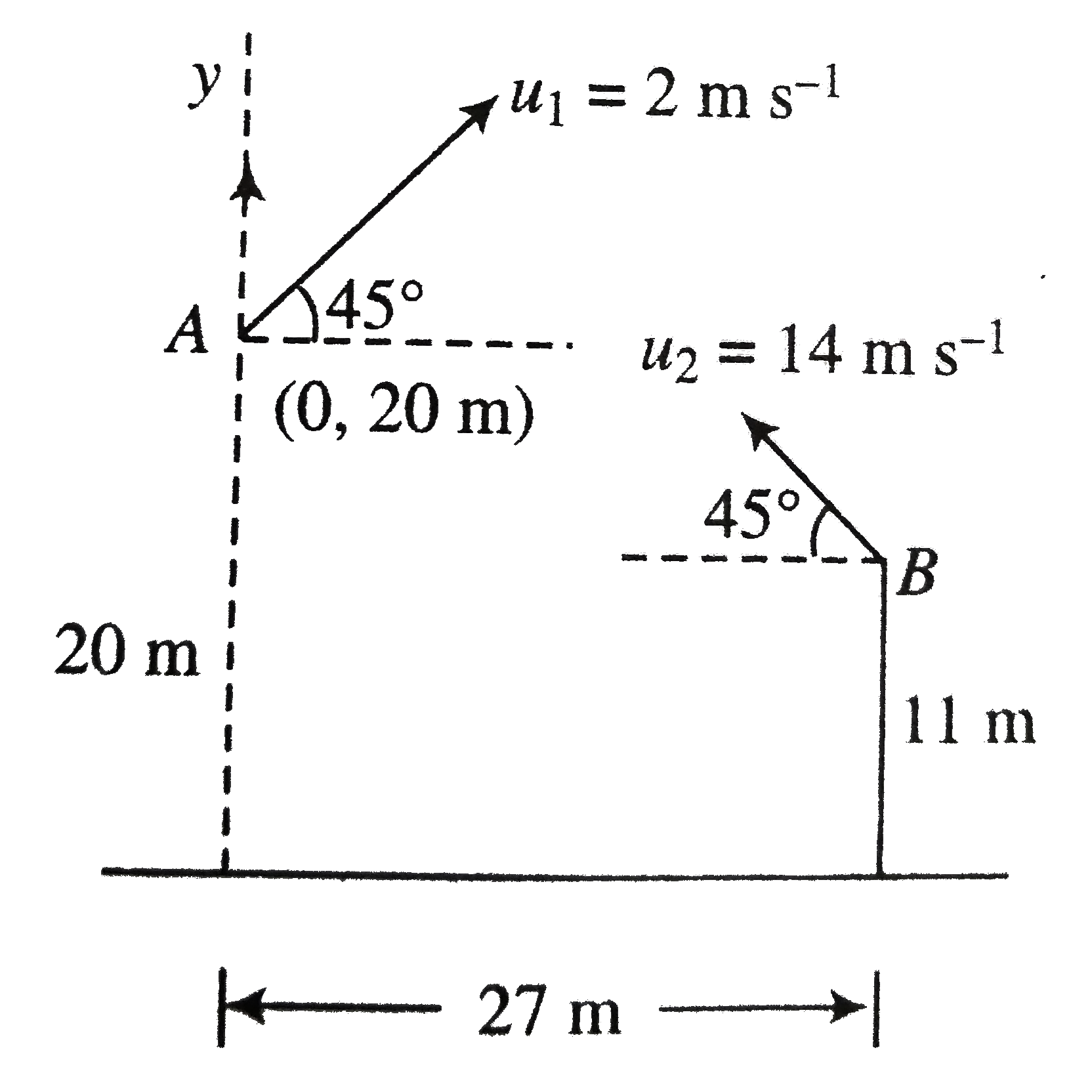
Minimum separation between A and B is
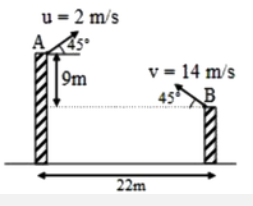
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
View SolutionTwo spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
View SolutionAn express train is moving with a velocity v1. Its driver finds another train is movig on the same track in the same direction with velocity v2. To escape collision, driver applies a retardation a on the train. The minimum time of escaping collision be
View SolutionTwo cars 1 and 2 move with velocities v1 and v2, respectively, on a straight road in same direction When the cars are separated by a distance d the driver of car 1 applies brakes and the car moves with uniform retardation a1, Simultaneously, car 2 starts accelerating with a2, If v1<v2, find the minimum initial separation between the cars to avoid collision between then.
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionA train is moving at a constant speed V when its driverobserves another train in front of him on the same track and voing in the same direction with constant speed v. If the distance berween the trains is x. Trains is x then what should be the minimum retardation of the train so as to avoed collision?.
View SolutionA particle starts moving with initial velocity u=25ms−1 and retardation a=−2ms−2. Draw the velocity-time graph.
View SolutionAn object is moving velocity 10ms−1 . A constant force acts for 4 s object and given it a speed of 2ms−1 in opposite direction. The acceleration produced is
View Solution

