If resistanceR1 in resistance box is 300Ω, then the balanced length is found to be 75.0cm from end A.The diameter of known wire is 1mm and length of the unknown wire is 31.4cm. Find the specific resistance of the unknown wire.
The correct Answer is:A, B, D
To find the specific resistance (resistivity) of the unknown wire, we will follow these steps:
Step 1: Understand the relationship in the potentiometer
The potentiometer works on the principle of a Wheatstone bridge, which states that the ratio of the resistances is equal to the ratio of the lengths of the wire. This can be expressed as:
R1Rx=L100−L
where R1 is the known resistance, Rx is the unknown resistance, L is the balanced length, and 100−L is the remaining length of the wire.
Step 2: Substitute the known values
Given:
- R1=300Ω
- L=75.0cm=0.75m
- Total length of wire =100cm=1.0m
We can calculate 100−L:
100−L=100cm−75cm=25cm=0.25m
Step 3: Calculate the unknown resistance Rx
Using the formula:
300Rx=0.750.25
Cross-multiplying gives:
300×0.25=Rx×0.75
75=0.75Rx
Now, solving for Rx:
Rx=750.75=100Ω
Step 4: Calculate the specific resistance (resistivity) of the unknown wire
The formula for resistance is:
R=ρLA
Where:
- R is the resistance,
- ρ is the specific resistance (resistivity),
- L is the length of the wire,
- A is the cross-sectional area.
The cross-sectional area A of the wire can be calculated using the diameter:
A=πD24
Given:
- Diameter D=1mm=1×10−3m
- Length of the unknown wire L=31.4cm=0.314m
Calculating the area:
A=π(1×10−3)24=π(1×10−6)4=π4×10−6m2
Step 5: Substitute values into the resistivity formula
Now substituting Rx=100Ω, L=0.314m, and A:
100=ρ(0.314)π4×10−6
Rearranging gives:
ρ=100×π4×10−60.314
Step 6: Calculate the specific resistance
Calculating the above expression:
ρ=100×0.7854×10−60.314≈2.5×10−4Ω⋅m
Final Answer
The specific resistance (resistivity) of the unknown wire is approximately:
ρ≈2.5×10−4Ω⋅m
---
The potentiometer works on the principle of a Wheatstone bridge, which states that the ratio of the resistances is equal to the ratio of the lengths of the wire. This can be expressed as:
R1Rx=L100−L
where R1 is the known resistance, Rx is the unknown resistance, L is the balanced length, and 100−L is the remaining length of the wire.
Given:
- R1=300Ω
- L=75.0cm=0.75m
- Total length of wire =100cm=1.0m
100−L=100cm−75cm=25cm=0.25m
Using the formula:
300Rx=0.750.25
Cross-multiplying gives:
300×0.25=Rx×0.75
75=0.75Rx
Now, solving for Rx:
Rx=750.75=100Ω
The formula for resistance is:
R=ρLA
Where:
- R is the resistance,
- ρ is the specific resistance (resistivity),
- L is the length of the wire,
- A is the cross-sectional area.
A=πD24
Given:
- Diameter D=1mm=1×10−3m
- Length of the unknown wire L=31.4cm=0.314m
A=π(1×10−3)24=π(1×10−6)4=π4×10−6m2
Now substituting Rx=100Ω, L=0.314m, and A:
100=ρ(0.314)π4×10−6
Rearranging gives:
ρ=100×π4×10−60.314
Calculating the above expression:
ρ=100×0.7854×10−60.314≈2.5×10−4Ω⋅m
The specific resistance (resistivity) of the unknown wire is approximately:
ρ≈2.5×10−4Ω⋅m
Topper's Solved these Questions
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.1
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.2
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
Similar Questions
If resistance R1 in resistance box is 300Ω then the balanced length is found to be 75.0cm from end A. The diameter of unknown wire is 1 mm and length of the unknown wire is 31.4cm. Find the specific resistance of the unknown wire
View SolutionIf resistance S in RB=300Ω, then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of the unknown wire is 3.14cm. The specific resistivity of the wire should be
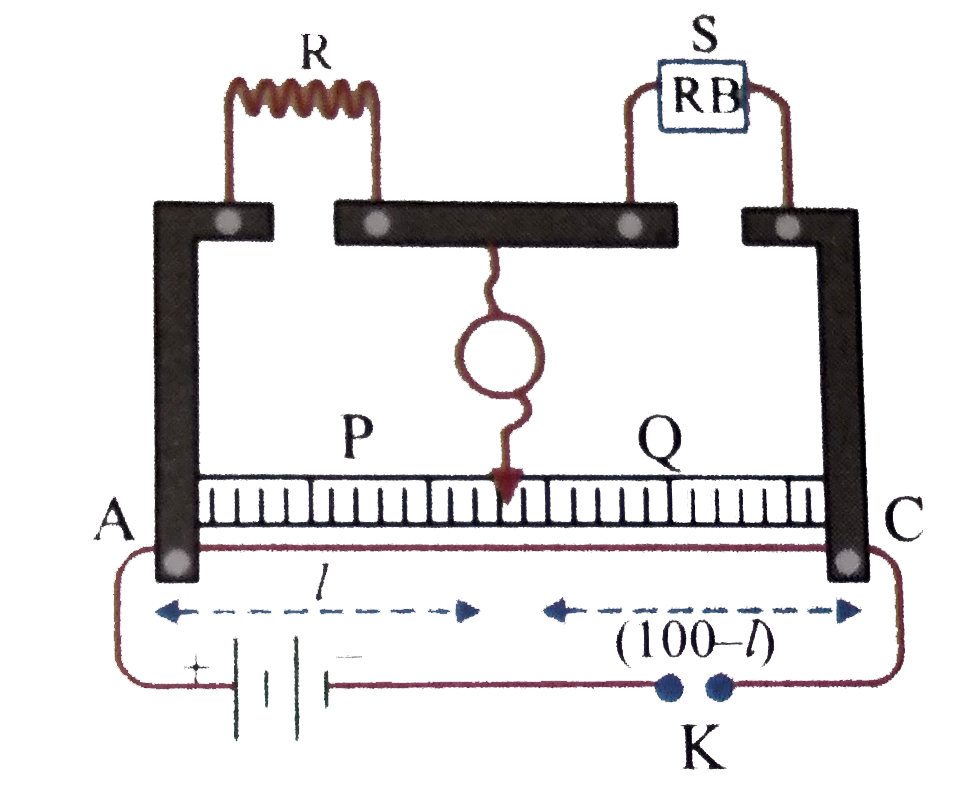
View SolutionIn meter bridge experiment if, resistance S in resistance box =300Ω then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of unknown wire is 31.4cm. The specific resistivity of the wire should be
View SolutionIf a wire is stretched to four times its length, then the specific resistance of the wire will
View SolutionIf the resistance of potentiometer wire is 15r then calculate the balance length l
View SolutionIf a wire is stretched to double its length, find the new resistance if the original resistance of the wire was R.
View SolutionIf the length of wire is (100.0 cm) and radius of wire as measured from screw gauge is (1.00mm) then the specific resistance of wire material is .
View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
View SolutionIn a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View SolutionWhen the switch is open in lowerpoint loop of a potentiometer, the balance point length is 60cm. When the switch is closed with a known resistance of R=4Ω the balance point length decreases to 40cm. Find the internal resistance of the unknown battery.
View Solution