In a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the given data
- EMF of the driver cell (E1) = 2 V
- Internal resistance of the driver cell (r1) = 0.5 Ω
- Length of the potentiometer wire (L) = 1 m
- EMF of the cell being measured (E2) = 1 V
- Internal resistance of the cell being measured (r2) = 0.5 Ω
- Length of wire balanced against the cell (l) = 60 cm = 0.6 m
Step 2: Calculate the current (I) in the primary circuit
The total resistance in the primary circuit is the sum of the resistance of the potentiometer wire (R) and the internal resistance of the driver cell (r1).
Using Ohm's law, the current (I) in the primary circuit can be calculated as:
I=E1R+r1
Substituting the values:
I=2R+0.5
Step 3: Calculate the potential difference across the length of the potentiometer wire
The potential difference across the length of the wire (V) can be expressed as:
V=I⋅R
Since the wire length is 1 m, the potential gradient (k) can be expressed as:
k=VL=I⋅R1=I⋅R
Step 4: Calculate the potential difference across the 60 cm length
For the cell with EMF 1 V balanced against 60 cm of the wire, the potential difference across this length can be expressed as:
V2=E2=1 V
The potential gradient can also be expressed as:
k=E2l=10.6
Step 5: Set the two expressions for potential gradient equal to each other
Since the potential gradient is the same for both cases, we can equate them:
I⋅R=10.6
Step 6: Substitute the expression for I from Step 2
Substituting the expression for I from Step 2 into the equation:
2R+0.5⋅R=10.6
Step 7: Solve for R
Cross-multiplying gives:
2R=10.6(R+0.5)
Expanding and simplifying:
2R=R0.6+0.50.6
Multiplying through by 0.6 to eliminate the fraction:
1.2R=R+0.5
Rearranging gives:
1.2R−R=0.5
0.2R=0.5
So,
R=0.50.2=2.5Ω
Final Answer
The resistance of the potentiometer wire is 2.5 Ω.
- EMF of the driver cell (E1) = 2 V
- Internal resistance of the driver cell (r1) = 0.5 Ω
- Length of the potentiometer wire (L) = 1 m
- EMF of the cell being measured (E2) = 1 V
- Internal resistance of the cell being measured (r2) = 0.5 Ω
- Length of wire balanced against the cell (l) = 60 cm = 0.6 m
The total resistance in the primary circuit is the sum of the resistance of the potentiometer wire (R) and the internal resistance of the driver cell (r1).
I=E1R+r1
Substituting the values:
I=2R+0.5
The potential difference across the length of the wire (V) can be expressed as:
V=I⋅R
Since the wire length is 1 m, the potential gradient (k) can be expressed as:
k=VL=I⋅R1=I⋅R
For the cell with EMF 1 V balanced against 60 cm of the wire, the potential difference across this length can be expressed as:
V2=E2=1 V
The potential gradient can also be expressed as:
k=E2l=10.6
Since the potential gradient is the same for both cases, we can equate them:
I⋅R=10.6
Substituting the expression for I from Step 2 into the equation:
2R+0.5⋅R=10.6
Cross-multiplying gives:
2R=10.6(R+0.5)
Expanding and simplifying:
2R=R0.6+0.50.6
Multiplying through by 0.6 to eliminate the fraction:
1.2R=R+0.5
Rearranging gives:
1.2R−R=0.5
0.2R=0.5
So,
R=0.50.2=2.5Ω
The resistance of the potentiometer wire is 2.5 Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:Try Yourself
Explore 34 Videos
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
Explore 69 Videos
- COMMUNICATION SYSTEMS Book:AAKASH INSTITUTE ENGLISHChapter:COMMUNICATION SYSTEMS Exercise:ASSIGNMENT SECTION D (Assertion-Reason)
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
The length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThe potentiometer wire is of length 1200 cam and it carries a current of 60 mA. For a cell of emf 5V and internal resistance of 20Ω, the null point of it is found to be at 1000 cm.The resistance of potentiometer wire is
View Solution
Knowledge Check
The potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
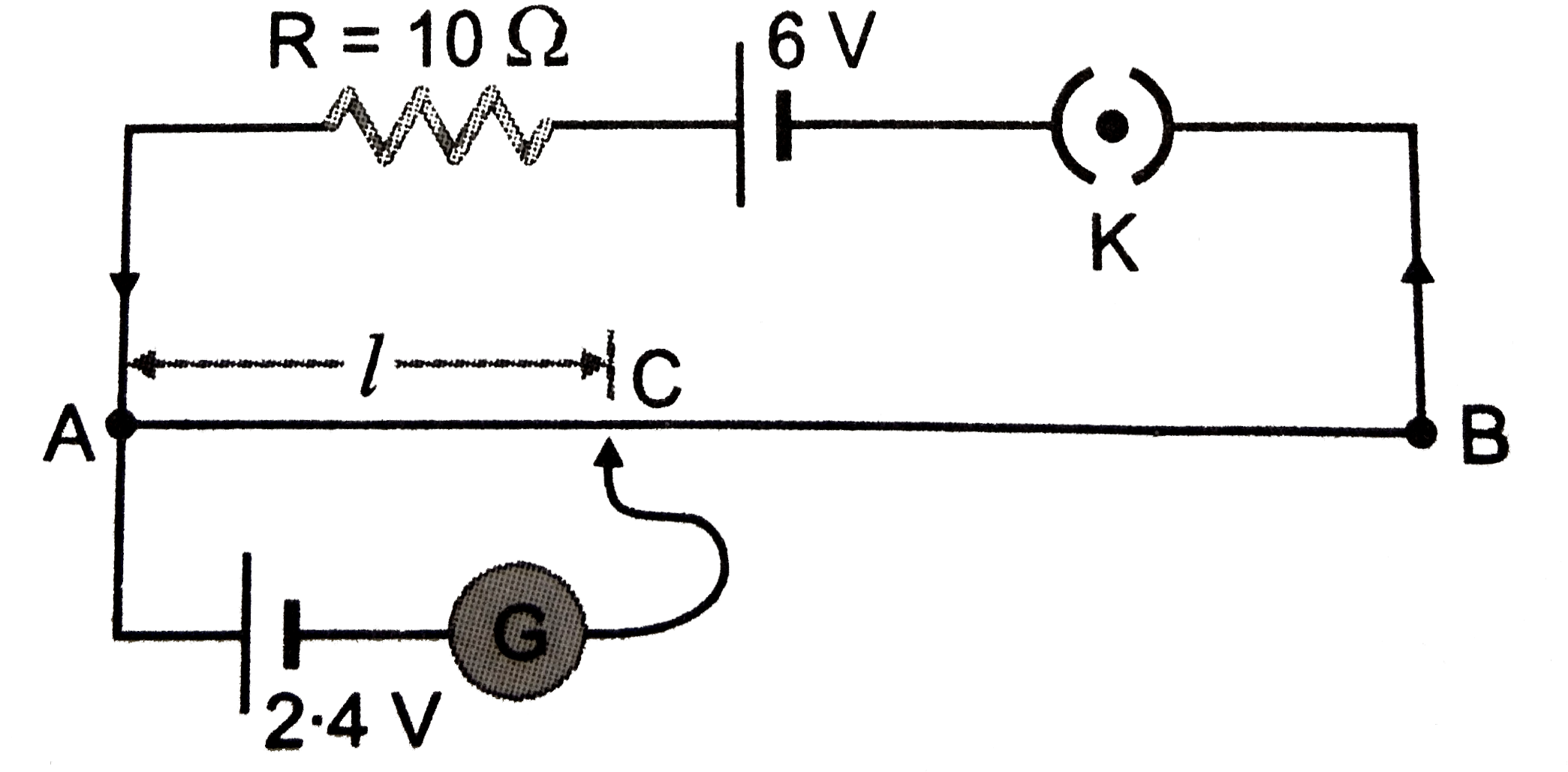 A100cmB120cmC110cmD140cm
A100cmB120cmC110cmD140cm
There is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
View SolutionA potentiometer arrangement is shows in Fig. 6.62. The driver cell has emf e and internal resistance r. The resistance of potentiometer wire AB is R.F is the cell of emf e/3 and internal resistance r/3. Balance point (J) can be obtained for all finite value of
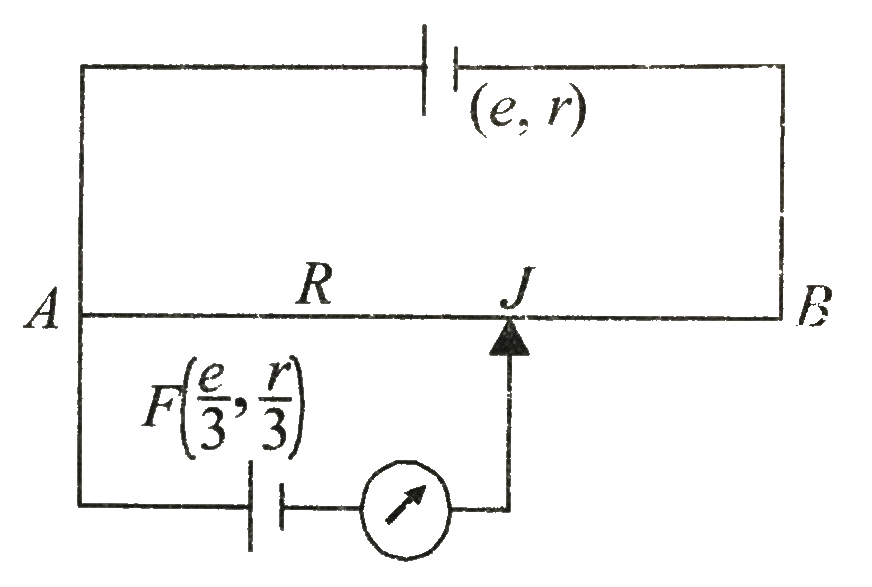
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionPassage - II :
Consider a potentiometer arrangement having auniform wire AB of resistance 99Ω
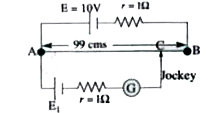
A driving battery of 10V emf and 1Ω internal resistance is used in the potentiometer. A cell of unknown emf E1 and internal resistance of 1Ω is balanced agains AC length of potentiometer wire.
When jockey is touched with wire AB at point C such that AC = 40 cm, there is no deflection in galvanometer. The emf of cell is
View SolutionA potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA 10 m long potentiometer wire carries a steady current. A standard cell of emf 1.018 V is balanced against a length of 254.5 cm of the wire. What is the potential gradient across the potentiometer wire ?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View Solution

