[1−1n+1]+[1−2n+1]+....+[1−nn+1]=?
0
n
1
n/2
The correct Answer is:D
Step by step video, text & image solution for [1-(1)/(n+1)] + [1-(2)/(n+1)] + ....+[1-(n)/(n+1)]=? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
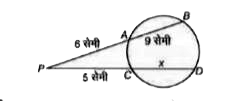
दी गई आकृति में x का मान ज्ञात कीजिए।
View Solutionयदि 25x−19−[3−{4x−5}]=3x−(6x−5) हो, तो x का मान है
View SolutionIf A=⎡⎢⎣111111111⎤⎥⎦, prove that An=⎡⎢ ⎢⎣3n−13n−13n−13n−13n−13n−13n−13n−13n−1⎤⎥ ⎥⎦,n∈N.
View SolutionProve that (1)/(n!)+(1)/(2!(n-2)!)+(1)/(4!(n-4)!)+...=(1)/(n!)2^(n-1)
View SolutionThe sequence where a_(n)=(1)/(n+1)+(1)/(n+2)+(1)/(n+3)+......+(1)/(n+n) is
View SolutionThe arithmetic mean of the series 1, 2, 4, 8, 16, ..... 2n is 2n−1n+1 (b) 2n+1n (c) 2n−1n (d) 2n+1−1n+1
View Solutionlimn−>∞[(1+1n)(1+2n)(1+nn)]1n
View SolutionThe sum of the series 11!(n−1)!+13!(n−3)!+15!(n−5)!+…..+1(n−1)!1! is = (A) 1n!2n (B) 2nn! (C) 2n−1n! (D) 1n!2n−1
View Solution((n+2)!+(n+1)(n-1)!)/((n+1)(n-1)!)=
View Solution(1−1n+1)+(1−2n+1)+(1−3n+1)+…….+(1−nn+1) का योग ज्ञात करें।
View Solutionयदि A = ⎡⎢⎣111111111⎤⎥⎦, तो सिद्ध कीजिए कि An=⎡⎢ ⎢⎣3n−13n−13n−13n−13n−13n−13n−13n−13n−1⎤⎥ ⎥⎦ , n∈N
View SolutionEvaluate limn→∞[(1+1n)(1+2n)⋅⋅⋅(1+nn)]1n
View SolutionIf 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!=(n+1)!−1 then show that, 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!+(n+1)(n+1)!=(n+2)!−1
View SolutionLet Sn=1+12+13+….+1n Show that nsn=n+(n−11+n−22+………+2n−2+1n−1).
View SolutionShow :
2n−n1!.2n−1+n(n−1)2!.2n−2−....+(−1)n=1
View Solutionদেখাও যে,(ii)2n−n1!2n−1+n(n−1)2!2n−2−...+(−1)n=1
View Solution
