(1−1n+1)+(1−2n+1)+(1−3n+1)+…….+(1−nn+1) का योग ज्ञात करें।
n
12n
(n+1)
12(n+1)
The correct Answer is:B
(1−1n+1)+(1−2n+1)+
=(1−3n+1)+………….+(1−n(n+1))
=n−1+2+3……….nn+1
=n−n(n+1)2(n+1)
{1+2+3………….n=n(n+1)2}
=n=n2=n2
Topper's Solved these Questions
Similar Questions
What sum of money must be given at simple interest for six months at 4% per annum in order to earnn 150 interest(रु 150 बियाज प्राप्त करने के लिए कितने रूपए को 6 महीने करने के लिए 4 % बियाज दर से साधारण बियाज पर देना होगा )
View SolutionA motorist and a scooterist made a journey of 120 km at the same time and from the same place. The graph shows the progress of the journey made by each person. Study the graph and answer the question.
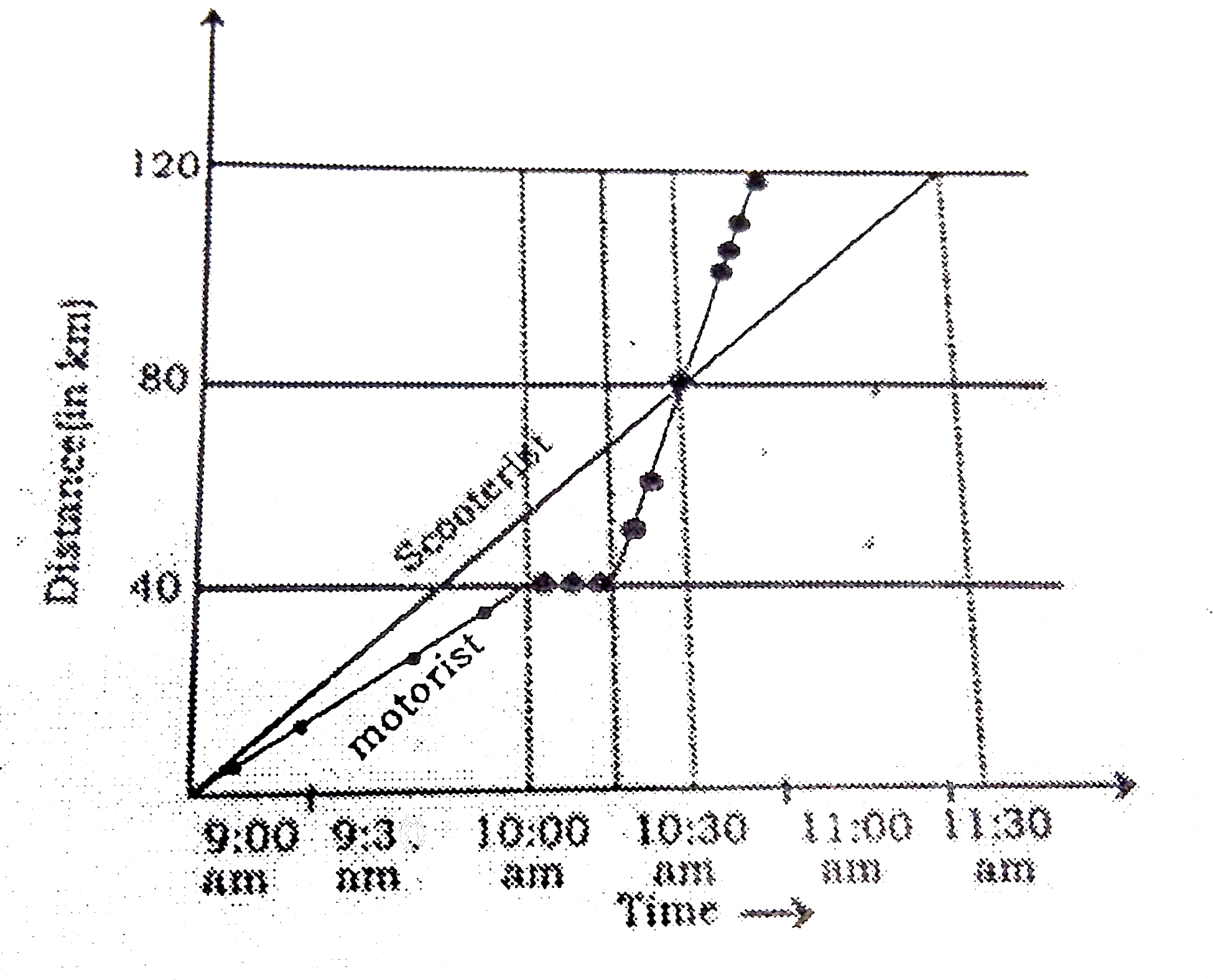
किस समय पर मोटर साइकिल वाला स्कूटर चालक से मिला ?
View SolutionIf A=⎡⎢⎣111111111⎤⎥⎦, prove that An=⎡⎢ ⎢⎣3n−13n−13n−13n−13n−13n−13n−13n−13n−1⎤⎥ ⎥⎦,n∈N.
View SolutionIf A,=[[1,1,11,1,11,1,1]]A^(n)=,[[3^(n-1),1]]3^(n-1),3^(n-1),3^(n-1)3^(n-1),3^(n-1),3^(n-1)]]
View SolutionThe sequence where a_(n)=(1)/(n+1)+(1)/(n+2)+(1)/(n+3)+......+(1)/(n+n) is
View SolutionThe sum of the series 11!(n−1)!+13!(n−3)!+15!(n−5)!+…..+1(n−1)!1! is = (A) 1n!2n (B) 2nn! (C) 2n−1n! (D) 1n!2n−1
View Solution((n+2)!+(n+1)(n-1)!)/((n+1)(n-1)!)=
View SolutionSimplify: (3^(n+1))/(3^(n(n-1)))-:(9^(n+1))/((3^(n+1))^((n-1)))
View Solutionयदि A = ⎡⎢⎣111111111⎤⎥⎦, तो सिद्ध कीजिए कि An=⎡⎢ ⎢⎣3n−13n−13n−13n−13n−13n−13n−13n−13n−1⎤⎥ ⎥⎦ , n∈N
View SolutionIf 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!=(n+1)!−1 then show that, 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!+(n+1)(n+1)!=(n+2)!−1
View SolutionLet Sn=1+12+13+….+1n Show that nsn=n+(n−11+n−22+………+2n−2+1n−1).
View Solutionनिम्नलिखित श्रेणियों का n पदों तक योग ज्ञात कीजिए :
11.2.3+12.3.4+13.4.5+…..............
View SolutionEvaluate :
limn→∞[(1+1n)(1+2n)(1+3n)…(1+nn)]1n
View Solution121.2+12+222.3!+12+22+323.4!+….+12+22+…+n2n.(n+1)!+…∞ का योग होगा।
View SolutionIf A=⎡⎢⎣111111111⎤⎥⎦, prove that An=⎡⎢ ⎢⎣3n−13n−13n−13n−13n−13n−13n−13n−13n−1⎤⎥ ⎥⎦,n∈N.
View Solution
