यदि n संख्याओं x1,x2,x3,.....,xn का समान्तर माध्य x हो, तो n∑i=1(xi−x)=?
0
n
1
n(x1+x2+x3+....+xn)
The correct Answer is:A
Step by step video, text & image solution for यदि n संख्याओं x_1 , x_2, x_3 , ....., x_n का समान्तर माध्य x हो, तो sum_(i=1)^(n)(x_i -x) = ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
दी गई आकृति में x का मान ज्ञात कीजिए।
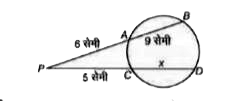
View Solutionयदि 25x−19−[3−{4x−5}]=3x−(6x−5) हो, तो x का मान है
View SolutionIf x1,x2,.......,xn are n values of a variable X such that n∑i=1(xi−2)=110 and n∑i=1(xi−5)=20. Find the value of n and the mean.
View SolutionIf x1,x2,x3….,xn are in H.P. prove that x1x2+x2x3+x3x4+……….+xn−1xn=(n−1)x1xn
View Solutionn प्रेक्षणों x1,x2,x3...., xn का माध्य तथा प्रसरण क्रमशः 5 तथा 0 हैं। यदि n∑i=1x2i=400, तब n का मान है
View SolutionIf x1,x2,.......,xn are n values of a variable X such that n∑i=1(xi−2)=110 and sum_(i=1)^n(x_i-5) =20. Find the value of n and the mean.
View SolutionIf the mean of n observation ax1,ax2,ax3,,axn is a¯¯¯X , show that (ax1−a¯¯¯X)+(ax2−a¯¯¯X)++(axn−a¯¯¯X)=0
View Solutionx1,x2,x3,……….,xn are n observations . n∑i=1(xi−2)=100 and n∑i=1(xi−5)=20 then mean ¯x = …….
View SolutionIf n observation x_1,x_2,.....,x_n The mean of is denoted by 7, then sum_(i=1)^(n) (x_i - bar(x)) The value of.
View SolutionLet x1,x2,x3,…xn be n values of a variable x. If these values are changed to x1+a,x2+a,…xn+a, where a∈ R, show that the variance remains unchanged.
View SolutionIf ¯x is the mean of a set of n observations x1,x2,x3…..,xn then n∑i=1(xi−¯x) is equal to
View SolutionIf x1,x2,x3,........xn are the roots of xn+ax+b=0, then the value of (x1−x2)(x1−x3)(x1−x4).......(x1–xn) is equal to
View SolutionIf X is discrete random variable takes the values x1,x2,x3, ... xn then ∑i=1P(xi)=........
View SolutionIfx1,x2,.....xn are n observations such that n∑i=1(xi)2=400 and n∑i=1xi=100 then possible values of n among the following is
View SolutionIf ¯x, is the mean of x1, x2, x3,…………..xn (n items) then nΣi=1(Xi−¯¯¯X)=...........
View SolutionIf x1,x2,x3….,xn are in H.P. prove that x1x2+x2x3+x3x4+……….+xn−1xn=(n−1)x1xn
View Solution
