When two soap bubbles of radii a and b (b>a) coalesce, the radius of curvature of common surface is :
a+bab
aba+b
b−aab
abb−a
To solve the problem of finding the radius of curvature of the common surface when two soap bubbles of radii a and b (where b>a) coalesce, we can follow these steps:
1. Understand the Concept of Excess Pressure in Soap Bubbles:
The excess pressure P inside a soap bubble is given by the formula:
P=4TR
where T is the surface tension and R is the radius of the bubble.
2. Identify the Excess Pressures for Both Bubbles:
For the smaller bubble with radius a:
P1=4Ta
For the larger bubble with radius b:
P2=4Tb
3. Determine the Relationship Between the Excess Pressures:
Since the excess pressure is inversely proportional to the radius, we have:
P_1 > P_2 \quad \text{(because a < b )}
4. Define the Excess Pressure at the Common Surface:
Let P be the excess pressure at the common surface of the two bubbles. The difference in excess pressures can be expressed as:
P1−P2=P
5. Substituting the Values of Excess Pressures:
Substitute the expressions for P1 and P2:
4Ta−4Tb=P
6. Simplifying the Equation:
Factor out 4T:
4T(1a−1b)=P
7. Finding the Radius of Curvature of the Common Surface:
The excess pressure at the common surface can also be expressed in terms of its radius of curvature R:
P=4TR
Setting the two expressions for P equal gives:
4TR=4T(1a−1b)
8. Canceling 4T from Both Sides:
1R=1a−1b
9. Rearranging the Equation:
1R=b−aab
10. Finding the Radius R:
Inverting both sides gives:
R=abb−a
Final Result
The radius of curvature of the common surface when the two soap bubbles coalesce is:
R=abb−a
The excess pressure P inside a soap bubble is given by the formula:
P=4TR
where T is the surface tension and R is the radius of the bubble.
For the smaller bubble with radius a:
P1=4Ta
For the larger bubble with radius b:
P2=4Tb
Since the excess pressure is inversely proportional to the radius, we have:
P_1 > P_2 \quad \text{(because a < b )}
Let P be the excess pressure at the common surface of the two bubbles. The difference in excess pressures can be expressed as:
P1−P2=P
Substitute the expressions for P1 and P2:
4Ta−4Tb=P
Factor out 4T:
4T(1a−1b)=P
The excess pressure at the common surface can also be expressed in terms of its radius of curvature R:
P=4TR
Setting the two expressions for P equal gives:
4TR=4T(1a−1b)
1R=1a−1b
1R=b−aab
Inverting both sides gives:
R=abb−a
The radius of curvature of the common surface when the two soap bubbles coalesce is:
R=abb−a
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION B)
30 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION A
60 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - (SECTION - B)
10 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
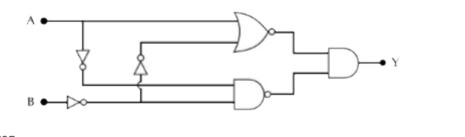
In the logic circuit shown in the figure, if input A and B are 0 to 1 respectively, the output at Y would be ‘x’
The value of x is _______
View SolutionThe position, velocity and acceleration of a particle moving with a constant acceleration can be represented by :
View SolutionA uniform metallic wire is elongated by 0.04 m when subjected to a linear force F. The elongation, if its length and diameter is doubled and subjected to the same force will be _____ cm.
View SolutionIf weight of an object at pole is 196 N then weight at equator is [g=10ms2 , radius of earth = 6400 Km]
View SolutionThe normal reaction 'N' for a vehicle of 800 kg mass, negotiating a turn on a 30∘ banked road at maximum possible speed without skidding is _______ ×103 kg m/s2.
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c . If the external pressure is P , find the surface tension of the soap solution.
View SolutionIf two soap bubbles of equal radii r coalesce then the radius of curvature of interface between two bubbles will be
View SolutionProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
View SolutionTwo spherical soap bubbles of radii a and b in vacuum coalesce under isothermal conditions. The resulting bubble has a radius given by
View Solutionजब r1 व r2त्रिज्या वाले साबुन के दो बुलबुले मिलते है तो उभयनिष्ठ सतह की वक्रता त्रिज्या होती है (r2>r1) -
View SolutionWhen two soap bubbles of radii r_1 and r_2 (r_2 lt r_1) adjoin, the radius of curvature of the common surface is
View SolutionTwo spherical soap bubbles of radii a and b in vacuum coalesce under isothermal condition. The resulting bubbles has a radius given by …..
View SolutionTwo spherical soap bubbles of radii a and b in vacuum coalesce under isothermal conditions. The resulting bubbles has a radius given by
View SolutionThe radii of two soap bubbles are R_(1)andR_(2) . If they coaleasce, then the radius of curvature of the common surface will be
View SolutionTwo soap bubbles of radii 4 cm and 5 cm coalesce to form a common surface. The radius of curvature of this common surface will be
View Solution
