A particle of mass m moves in a circular orbit under the central potential field, U(r)==−Cr, where C is a positive constant.
The correct radius -velocity graph of the particle's motion is.

To solve the problem of a particle of mass m moving in a circular orbit under the central potential field U(r)=−Cr, we need to analyze the relationship between the radius r and the velocity v of the particle.
1. Identify the Potential Energy:
The potential energy of the particle is given by:
U(r)=−Cr
where C is a positive constant.
2. Calculate the Force:
The force F acting on the particle can be derived from the potential energy using the relationship:
F=−dUdr
We differentiate U(r):
F=−ddr(−Cr)=Cr2
3. Centripetal Force Requirement:
For a particle moving in a circular orbit, the centripetal force required to keep it in that orbit is given by:
Fc=mv2r
Setting the centripetal force equal to the gravitational force we calculated:
mv2r=Cr2
4. Rearranging the Equation:
Multiplying both sides by r2 gives:
mv2=Cr
Rearranging this, we find:
v2=Cmr
5. Understanding the Relationship:
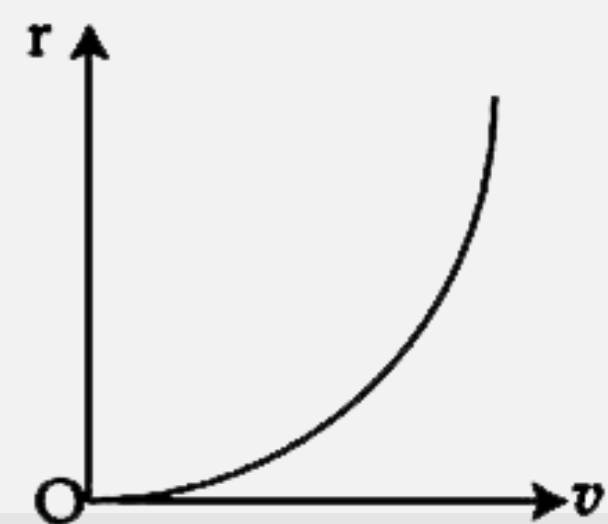
From the equation v2=Cmr, we can see that v2 is inversely proportional to r. Therefore, as r increases, v2 decreases, which implies that v decreases as r increases.
6. Graphical Representation:
The relationship v2∝1r suggests that if we plot v against r, the graph will be a downward curve (hyperbolic shape). Specifically, it indicates that the velocity decreases as the radius increases.
7. Identifying the Correct Option:
Among the given options, we need to look for a graph that shows a decreasing trend in velocity as the radius increases. The correct graph will show that as r increases, v decreases, confirming the inverse relationship.
Conclusion:
The correct radius-velocity graph of the particle's motion is the one that shows a downward curve, indicating that as the radius r increases, the velocity v decreases.
---
The potential energy of the particle is given by:
U(r)=−Cr
where C is a positive constant.
The force F acting on the particle can be derived from the potential energy using the relationship:
F=−dUdr
We differentiate U(r):
F=−ddr(−Cr)=Cr2
For a particle moving in a circular orbit, the centripetal force required to keep it in that orbit is given by:
Fc=mv2r
Setting the centripetal force equal to the gravitational force we calculated:
mv2r=Cr2
Multiplying both sides by r2 gives:
mv2=Cr
Rearranging this, we find:
v2=Cmr
From the equation v2=Cmr, we can see that v2 is inversely proportional to r. Therefore, as r increases, v2 decreases, which implies that v decreases as r increases.
The relationship v2∝1r suggests that if we plot v against r, the graph will be a downward curve (hyperbolic shape). Specifically, it indicates that the velocity decreases as the radius increases.
Among the given options, we need to look for a graph that shows a decreasing trend in velocity as the radius increases. The correct graph will show that as r increases, v decreases, confirming the inverse relationship.
The correct radius-velocity graph of the particle's motion is the one that shows a downward curve, indicating that as the radius r increases, the velocity v decreases.
Similar Questions
A particle of mass m moves under the action of a central force. The potential energy function is given by U(r)=mkr3 Where k is a positive constant and r is distance of the particle from the centre of attraction. (a) What should be the kinetic energy of the particle so that it moves in a circle of radius a0 about the centre of attraction? (b) What is the period of this circualr motion ?
View SolutionA particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
View Solution
Knowledge Check
A particle of mass m moves in circular orbits with potential energy N(r)=Fr, wjere F is a positive constant and r its distance from the origin. Its energies are calculated using the Bohr model. If the radius of the the nth orbit (here h is the Planck's constant)
ARαn1/3 and vαn2/3BRαn2/3 and vαn1/3CE=32(n2h2F24π2m)1/3DE=2(n2h2F24π2m)1/3A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance r. The speed of the particle is
AProportional to r2BIndependent of rCProportional to rDProportional to 1/rA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
AT/R is constantBTR is a constantCT2/R3is a constantDT/R2 is a constant
A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
View SolutionA particle of mass m moves in a circular orbit in a central potential field U(r)=U0r4. If Bohr's quantization conditions are applied, radü of possible orbitals rn vary with n1α, where α is _________.
View SolutionA particle of mass m moves in a circular orbit in a central potential field
U(r)=12Kr2. If Bohr's quantization conditions are applied , radii of possible orbitls and energy levels vary with quantum number n as :
View SolutionA small particle of mass m, moves in such a way that the potential energy U=ar3, where a is position constant and r is the distance of the particle from the origin. Assuming Rutherford's model of circular orbits, then relation between K.E and P.E of the particle is :
View SolutionTwo particles of identical mass are moving in circular orbits under a potential given by V(r)=Kr−n, where K is a constant. If the radii of their orbits are r1,r2 and their speeds are v1,v2, respectively, then
View Solution

