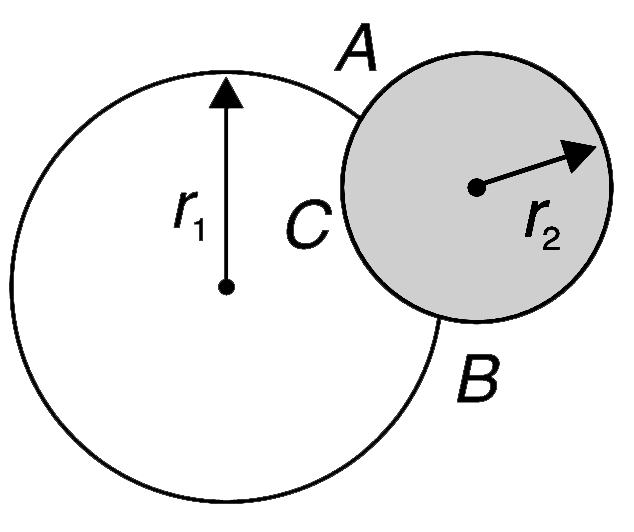
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
A
r2−r1
B
r2−r1r1r2
C
r1r2r2−r1
D
r2+r1
Video Solution
Text Solution
The correct Answer is:C
Radius of curvature of common surface is,
RCommon=r1r2r2−r1
|
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:B) Medical entrance special format question
Explore 19 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Match the columns
Explore 6 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Check point 13.4
Explore 10 Videos
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Knowledge Check
If two bubble of radii 0.03 cm and 0.04 cm come in contact with each other then the radius of curvature of the common surface 'r' is given by.
A0.03B0.06C0.12D0.24Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1Two circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
Aθ=sin−1(r1+r2r1−r2)Bθ=2sin−1(r1−r2r1+r2)Cθ=sin−1(r1−r2r1+r2)Dnone of these
Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionProve that r1+r2+r3−r=4R
View SolutionProve that r1+r2+r3−r=4R
View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
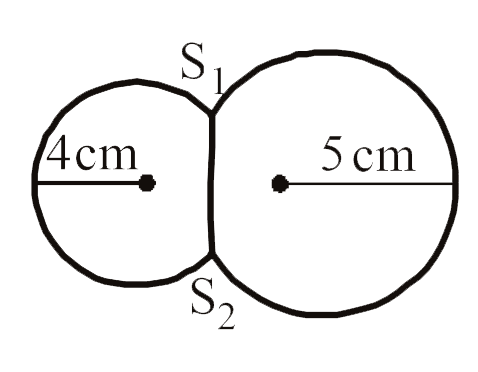
View Solution