Two parallel glass plates separated by a small distance x are dipped partly in a liquid of density " d" keeping them vertical .The surface tension of the liquid is T and angle of contact is θ . What is the rise of the liquid between the plates due to capillarity ?
Tcosθxd
2Tcosθxdg
2Txdgcosθ
Tcosθxdg
The correct Answer is:B
Let the width of each plate is b and due to surface tension liquid will rise upto height h, then upward force due to surface tension =2Tbcosθ

Weight of the liquid eises in betweent the plates
= Vdg = (bxh)dg
Equating Eqs. (i) and (ii), we get
2Tbcosθ=bxhdg
∴ h=2Tcosθxdg
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:B) Medical entrance special format question
Explore 19 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Match the columns
Explore 6 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Check point 13.4
Explore 10 Videos
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Two parallel plates which are sparated by a very small distance d, are dipped in water. To how much height will the water raise between the plates (Assume contact angle θ→0)
View SolutionA liquid of density ρ and surface tension S rises to a height h in a capillary tube of diameter D. what is the weight of the liquid in the capillary tube? Angle of contact is 0∘.
View Solution
Knowledge Check
Two parallel glass plates separated by a small distance x are dipped partly in a liquid of density " d" keeping them vertical .The surface tension of the liquid is T and angle of contact is θ . What is the rise of the liquid between the plates due to capillarity ?
ATcosθxdB2TcosθxdgC2TxdgcosθDTcosθxdgTwo parallel glass plates are dipped partly in the liquid of denstiy 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then ries of liquid between the plates due to capillary will be
ATcosθxdB2TcosθxdgC2TxdgcosθDtcosθxdgA capillary tube of radius r is dipped in a liquid of density ρ and surface tension S. if the angle of contanct is θ, the pressure difference between the two surface in the beaker and the capillary ?
ASrcosθB2SrcosθCSrcosθD2Srcosθ
Derive an expression for the height of capillary rise between two parrallel plates dipping in a liquid of density σ separated by a distance d. The surface tension of the liquid is T.
View Solution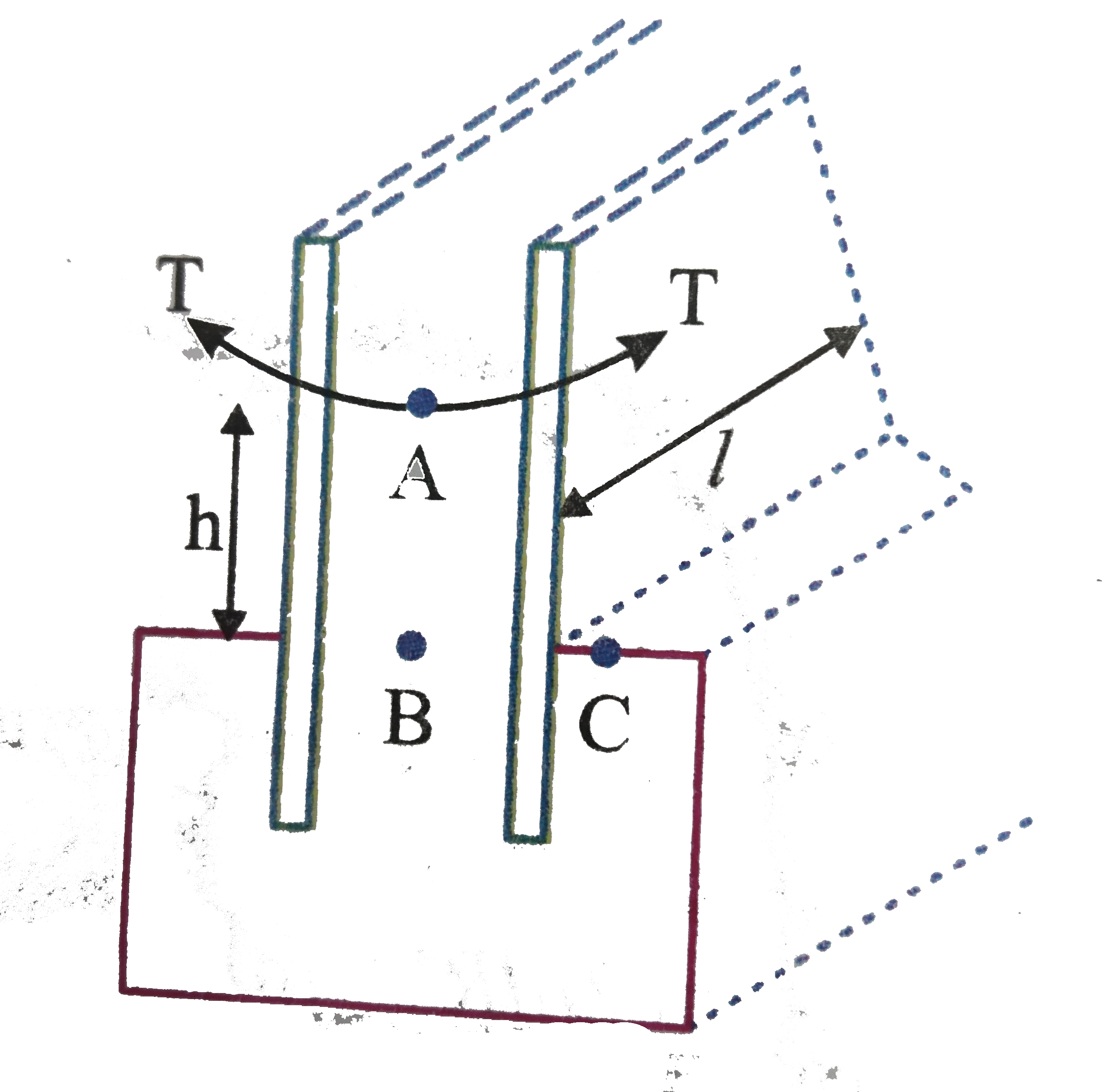
Expression for the height of capillary rise between two parallel plates dipping liquid of density σ separated by a distance d. The surface tension of the liquid is T. [Take angle of contact to be zero]
View SolutionTwo parallel glass plates are held vertically at a small separation d and dipped in a liquid of surface tension T , the angle of contact θ=0∘ and density ρ . The height of water that climbs up in the gap between glass plates is given by
View SolutionWhen the temperature of a liquid is increased , following changes take place in the surface tension (T) and angle of contact (θ)
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View Solution

