A small ball (mass m) falling under gravity in a viscous medium experience a drag force proportional to the instantaneous speed u such that Fdrag=ku. Then the terminal speed of ball within viscous medium is
kmg
mgk
√mgk
None of these
The correct Answer is:D
Weight-upthrust=dragforce.
But no information is given reagarding the upthrust.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A spherical body of diameter D is falling in viscous medium. Its terminal velocity is proportional to
View SolutionA small spherical ball falling under gravity in a viscous medium heat the medium due to viscous drage force. The rate of heating is proportional to rn. (r= radius of the sphere find )n.
View Solution
Knowledge Check
A small steel ball of mass m and radius r is falling under gravity through a viscous liquid of coefficient of viscosity η. If g is the value of acceleration due to gravity. Then the terminal velocity of the ball is proportional to (ignore buoyancy)
Amg(η)rBmg(η)rCmgrηDmgrηThe displacement of a ball falling rest in a viscous medium is platted against time. Choose a possible option
A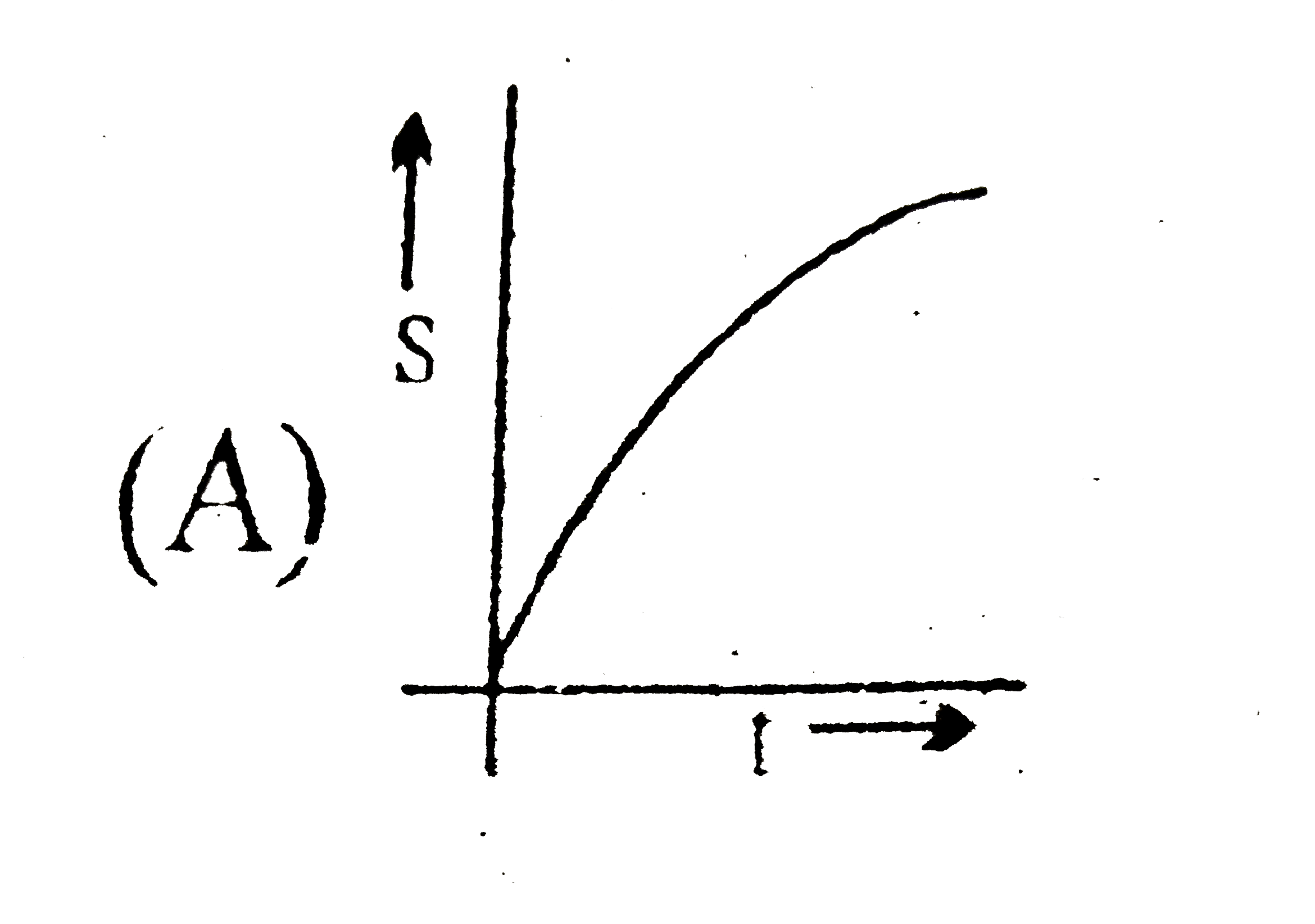 B
B C
C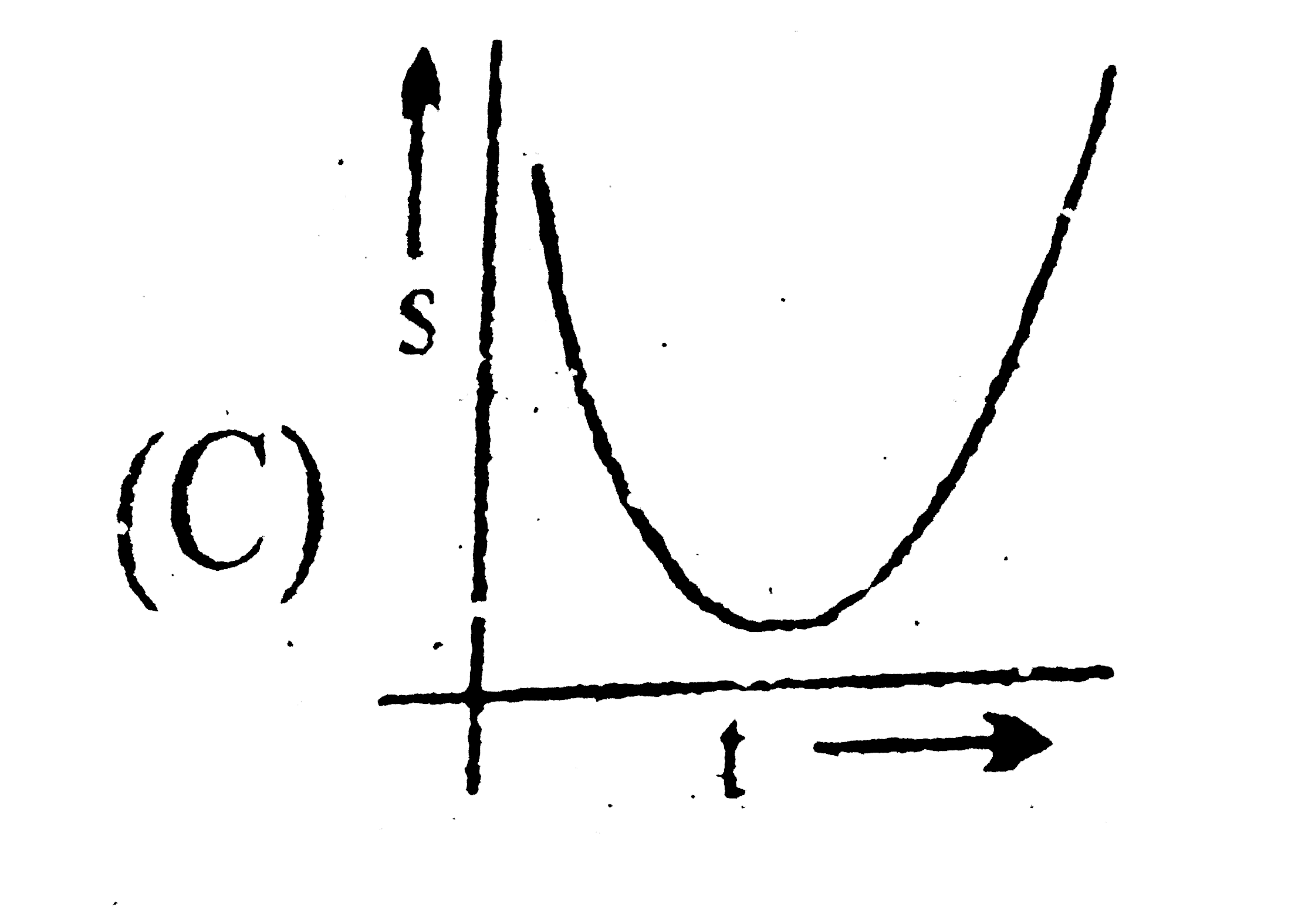 D
D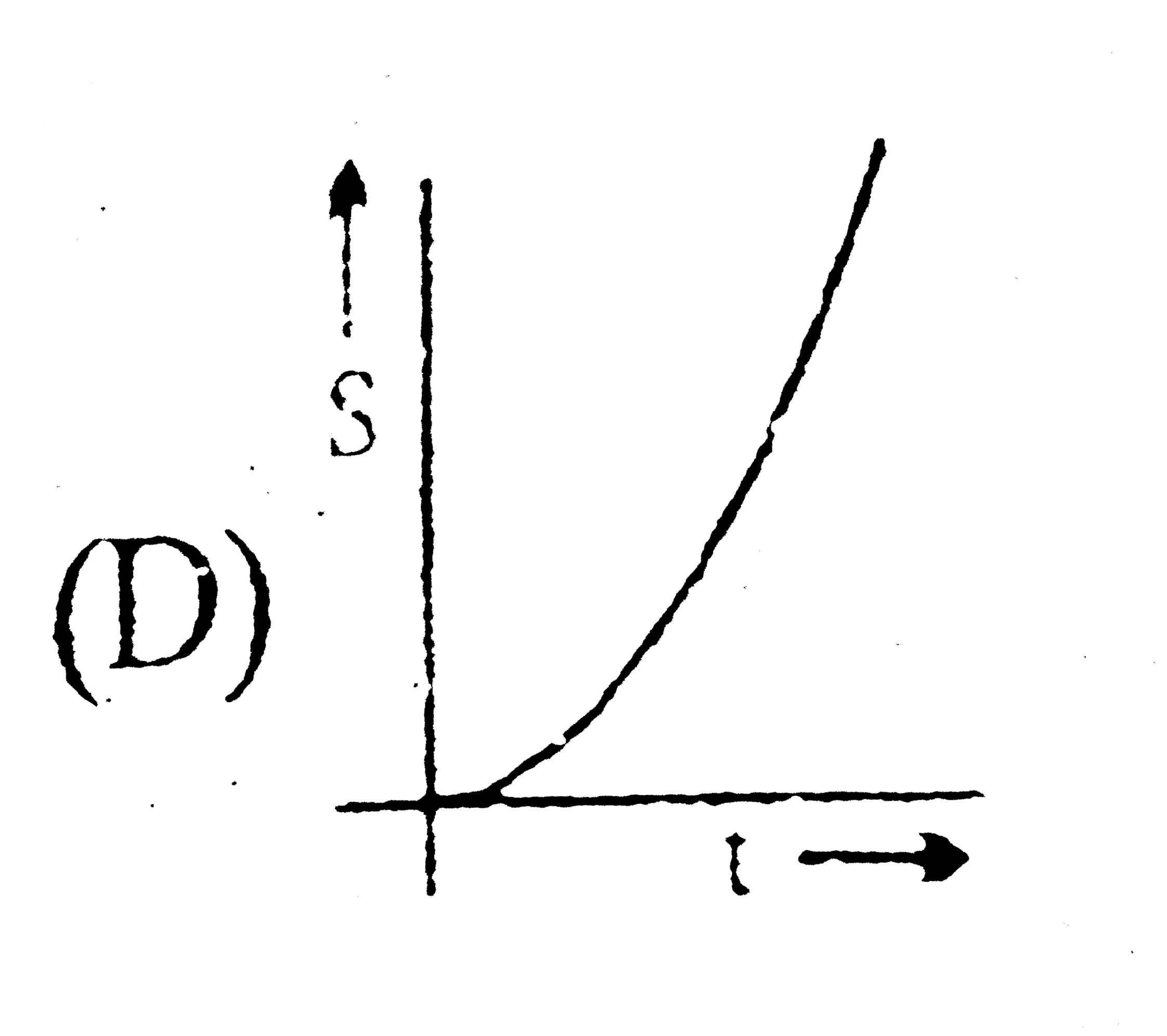
An oil drop of mass m fall through a viscous medium. The viscous drag force. F is proportional to the velocity of the drop . At the instant it begins to fall the force that acts on the oil drop is (neglect buoyancy)
AmgBmg−FCF−mgDF
A small spherical body of radius r is falling under gravity in a viscous medium. Due to friction the meduim gets heated. How does the rate of heating depends on radius of body when it attains terminal velocity?
View SolutionA small spherical ball falling through a viscous medium of negligible density has terminal velocity v. Another ball of the same mass but of radius twice that of the earlier falling through the same viscous medium will have terminal velocity
View SolutionA spherical metal ball of mass m and radius (r) is falling through a viscous medium. The value of its terminal velocity is proportional to
View SolutionA spherical solid ball of volume V is made of a material of density ρ1. It is falling through a liquid of density ρ2(ρ2<ρ1). Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., Fviscous=−kv2(k>0). The terminal speed of the ball is
View Solutionn small balls, each of mass m and velocity u strike elastically on a surface per second. The force exerted on the surface
View Solution
