Obtain the relation of phase between instantaneous current and voltage with the help of phase diagram for series LCR circuit. Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

In circuit L-C-R are in series. Therefore, the act current in each element is the same at any time having the same amplitude and phase.

Let it be $I = I_{m} sin (ω t + ϕ)$ …(1)
where $ϕ$ is the phase difference between the voltage across the source and the current in the circuit.
Let $\to I$ be the phasor representing the current in the circuit and $- \to V_{L}, - \to V_{C}, - \to V_{R}$ and $\to V$ represent the voltage across the inductor, resistor, capacitor and the source respectively.
$- \to V_{R}$ is parallel to $\to I$
$- \to V_{C}$ is $\frac{π}{2}$ behind $\to I$ and
$- \to V_{L}$ is $\frac{π}{2}$ ahead of $\to I$ .
$- \to V_{L}, - \to V_{C}, - \to V_{R}$ and $\to I$ are shown in figure with appropriate phase relation.

The amplitude of phasor are as follow.
$V_{R m} = I_{m} R, V_{C M} = I_{m} X_{c}, V_{L m} = I_{m} X_{L}$
The voltage equation for the circuit can be written as,
$L \frac{d I}{d t} + I R + \frac{q}{C} = V$ can be written as below
$- \to V_{L} + - \to V_{R} + - \to V_{C} = \to V$ where $V_{L} = L \frac{d I}{d t}, V_{R} = I R$ and $V_{C} = \frac{q}{C}$
$∴$ The phasor relation $- \to V_{L} + - \to V_{R} + - \to V_{C} = \to V$
This relation is represented in below figure.

Since $- \to V_{C}$ and $- \to V_{L}$ are in opposite directions, so the resultant value of phasor.
$- \to V_{C} - \to V_{1} = V_{C m} - V_{L m}$
Since $\to V$ is represented as the hypotenuse of a right triangle whose sides are $\to R$ and $- \to V_{C} + - \to V_{L}$ the Pythagorean theorem gives.
$V_{m}^{2} = V_{R m}^{2} + {(V_{C m} - V_{L m})}_{C m}^{2}$
$∴ V_{m}^{2} = {(I_{m} R)}_{m}^{2} + {[(I_{m} X_{C}) - (I_{m} X_{L})]}^{2}$
$∴ V_{m}^{2} = I_{m}^{2} [R^{2} + {(X_{C} - X_{L})}_{C}^{2}]$
$∴ I_{m}^{2} = \frac{V_{m}^{2}}{R^{2} + {(X_{C} - X_{L})}_{C}^{2}}$
$∴ I_{m} = \frac{V_{m}}{{[R^{2} + {(X_{C} - X_{L})}_{C}^{2}]}^{\frac{1}{2}}}$ but $\sqrt{R^{2} + {(X_{C} - X_{L})}_{C}^{2}} = Z$ where Z is called impedance.
$∴ I_{m} = \frac{V_{m}}{Z}$ is the amplitude of current.
Since phasor $\to I$ is always parallel to phaosr $- \to V_{R}$ the phase angle $ϕ$ is the angle between $- \to V_{R}$ and $\to V$ can be determined from figure,

$tan ϕ = \frac{V_{C m} - V_{L m}}{V_{R m}}$
$= \frac{I_{m} X_{C} - I_{m} X_{L}}{I_{m} R}$
$∴ tan ϕ = \frac{X_{C} - X_{L}}{R}$ gives phase angle.
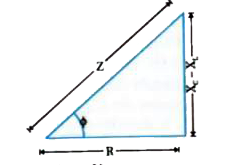
Impedance Z of circuit can be determined by figure. This is called impedance diagram which is a right triangle with Z as its hypotenuse.
Impedance from impedance diagram, $Z = \sqrt{R^{2} + {(X_{C} - X_{L})}_{C}^{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ALTERNATING CURRENTS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ALTERNATING CURRENTS -SECTION-A (QUESTIONS-ANSWERS)

Home
Ask Doubt
Profile