An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT. Pressure remaining constant. The physical quantity δ=ΔVVΔT varies with temperature as : Solution in Telugu
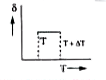
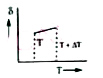
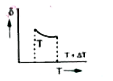
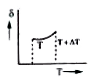
The correct Answer is:C
Step by step video, text & image solution for An ideal gas is initially at temperature T and volume V. Its volume is increased by Delta V due to an increase in temperature Delta T. Pressure remaining constant. The physical quantity delta = ( Delta V)/( V Delta T) varies with temperature as : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Boyle.s Law - applications)
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Kinetic theory of gases)
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF LIQUIDS (PRACTICE SHEET) LEVEL-II (Integer/Subjective Type Questions)
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH SERIESChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE EXERCISE
Explore 99 Videos
- THERMODYNAMICSBook:AAKASH SERIESChapter:THERMODYNAMICSExercise:EXERCISE - 3
Explore 33 Videos
Similar Questions
An air bubble comes from the bottom to the surface of a lake of depth 2.5 m. The surface temperature of the lake is 40∘C. The diameter of the bubble at the bottom and at the surface are 3.6 mm and 4 mm respectively. Find the temperature of the lake at the bottom.
View SolutionTwo thermally insulated vessels 1 and 2 are filled with air at temperature (T1,T2), volume (V1,V2) and pressure (P1,P2) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
View SolutionIn figure shown, left arm of a U-tube is immersed in a hot water bath at temperature T, and right arm is immersed in a bath of melting ice, the height of monomeric liquid in respective columns is htandh0. Determine the coefficient of expansion of the liquid

View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
View SolutionAn ideal gas is initially at temperature T and volume V . Its volume is increased by DeltaV due to an increase in temperature Delta , pressure remaining constant . The quantity delta=DeltaV//VDeltaT varies with temperature as
View Solutionएक आदर्श गैस का प्रारम्भ में आयतन V तथा ताप T है | ΔT ताप वृद्धि के कारण इसका आयतन ΔV बढ़ जाता है, जबकि दाब नियत रहता है | राशि δ=ΔVVΔT का ताप के साथ परिवर्तन का सही प्रदर्शन होगा
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
View SolutionAt constant pressure, the temperature coefficient of volume expansion of an ideal gas is delta = 1/V (dV)/(dT) . What will be the nature of the graph relating delta with the temperature T?
View SolutionAn ideal gas is initiaily at temperature T and volumoeV. lts volume is increased by Delta V due to an increase in temperature Delta T , pressure remaining constant. The quantity k = AV//(V Delta T) varies with temperature as:
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by DeltaV due to an increase in temperature DeltaT, pressure remaining constant. The quantity delta=(DeltaV)/(VDeltaT) varies with temperature as
View SolutionAn ideal gas is initially at temperature T and volume V. ITS volume is increased by DeltaV due to an increase in temperature DeltaT , pressure remaining constant. The quantity delta = DeltaV//V DeltaT varies with temperature as
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature DelatT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as :
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as :
View Solution

