An ideal gas is initially at temperature T and volume V . Its volume is increased by ΔV due to an increase in temperature Δ , pressure remaining constant . The quantity δ=ΔV/VΔT varies with temperature as
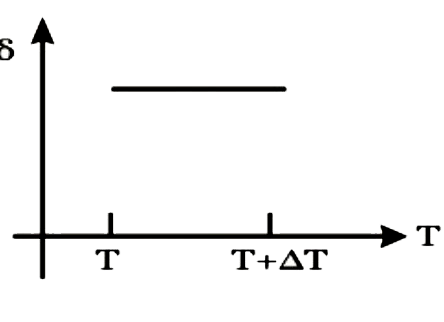
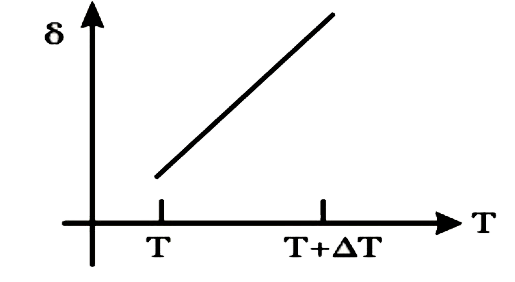

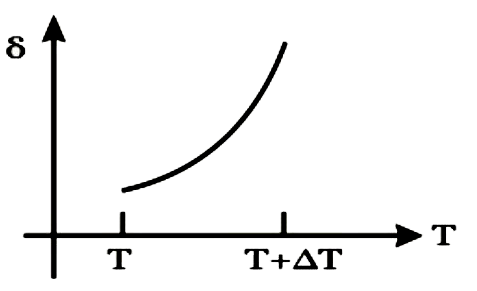
The correct Answer is:C
To solve the problem step by step, we will analyze the relationship between volume, temperature, and the given quantities in an isobaric process (constant pressure).
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Since the pressure is constant in this scenario, we can express the relationship between volume and temperature.
Step 2: Express Volume in Terms of Temperature
From the ideal gas law, if P is constant, we can write:
V∝T
This means that volume V is directly proportional to temperature T. We can express this as:
V=kT
Where k is a constant.
Step 3: Differentiate the Volume Equation
Now, we differentiate both sides of the equation V=kT:
dV=kdT
This equation shows how a small change in volume relates to a small change in temperature.
Step 4: Relate Changes in Volume and Temperature
Next, we can write the ratio of changes:
dVV=kdTkT
This simplifies to:
dVV=dTT
Step 5: Convert to Finite Changes
Since the problem mentions finite changes (denoted by Δ), we can replace d with Δ:
ΔVV=ΔTT
Step 6: Rearranging the Equation
We can rearrange the equation to express the relationship between ΔV, V, ΔT, and T:
ΔV⋅ΔT=VT
Step 7: Define the Quantity δ
The problem defines δ as:
δ=ΔVVΔT
Substituting from our previous result:
δ=1T
Step 8: Analyze the Relationship
From the equation δ=1T, we can see that δ is inversely proportional to the temperature T.
Conclusion
Thus, the quantity δ varies inversely with temperature T. If we were to graph this relationship, it would show a hyperbolic decline, indicating that as temperature increases, δ decreases.
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
From the ideal gas law, if P is constant, we can write:
V∝T
This means that volume V is directly proportional to temperature T. We can express this as:
V=kT
Where k is a constant.
Now, we differentiate both sides of the equation V=kT:
dV=kdT
This equation shows how a small change in volume relates to a small change in temperature.
Next, we can write the ratio of changes:
dVV=kdTkT
This simplifies to:
dVV=dTT
Since the problem mentions finite changes (denoted by Δ), we can replace d with Δ:
ΔVV=ΔTT
We can rearrange the equation to express the relationship between ΔV, V, ΔT, and T:
ΔV⋅ΔT=VT
The problem defines δ as:
δ=ΔVVΔT
Substituting from our previous result:
δ=1T
From the equation δ=1T, we can see that δ is inversely proportional to the temperature T.
Thus, the quantity δ varies inversely with temperature T. If we were to graph this relationship, it would show a hyperbolic decline, indicating that as temperature increases, δ decreases.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An ideal gas is initially at temperature T and volume V. It's volume increases by ΔV due to an increase in temperature of ΔT, pressure remaining constant. The quantity μ=ΔVVΔT varies with temperature as -
A B
B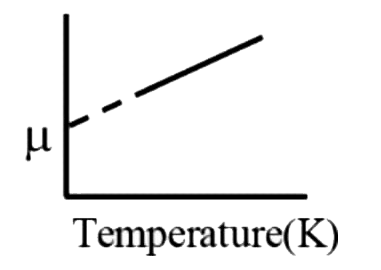 C
C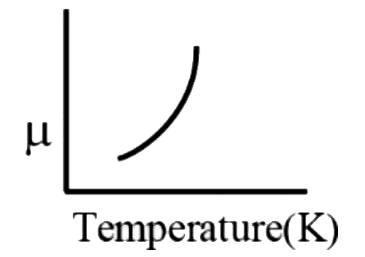 D
D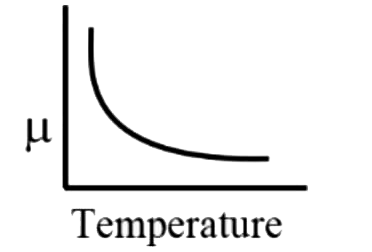
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A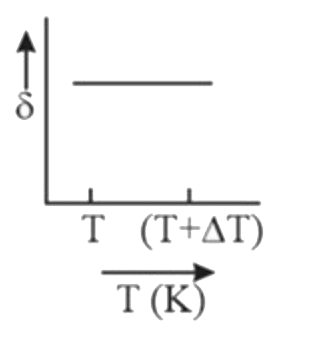 B
B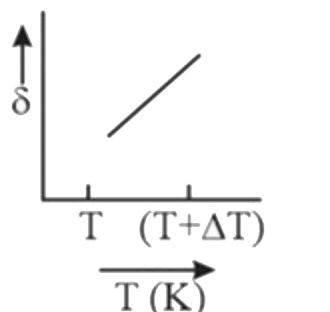 C
C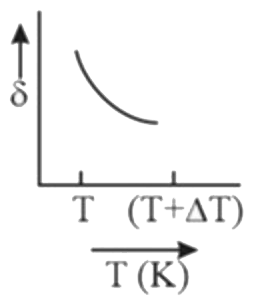 D
D
A constant temperature , the volume of a gas is to be decreased by 4 % The pressure must be increased by
A0.04B0.0416C0.08D0.0386
Pressure of a gas increases due to increase of its temperature because at higher temperature
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionAt constant volume, temperature is increased. Then
View SolutionThe volume of a gas is increasing adiabatically. Its temperature
View SolutionAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
View Solution
