The system shown in figure consists of three springs and two rods as shown. These springs are initially relaxed and there is no friction. The temperature of each of the rod is increased by ΔT. The coefficient of linear expansion of the material of rods is equal to α.

The energy stored in spring S is 81242kL2α(ΔT)2
The energy stored in spring S2 is 81484kL2α2(ΔT)2
The energy stored in spring S3 is 27242kL2α2(ΔT)2
No energy is stored in any of the springs.
The correct Answer is:A, B, C
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Linked Comprehension Type Questions
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF SOLIDS (LECTURE SHEET) Matrix Matching Type Questions
Explore 2 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:THERMOMETRY (PRACTICE SHEET) LEVEL-II (Integer/Subjective Type Questions)
Explore 3 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH SERIESChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE EXERCISE
Explore 99 Videos
- THERMODYNAMICSBook:AAKASH SERIESChapter:THERMODYNAMICSExercise:EXERCISE - 3
Explore 33 Videos
Similar Questions
The system shown in figure consists of three springs and two rods as shown. If the temperature of the rods is increased by δ(t) calculate the energy stored in each of the springs. The springs are initially relaxed. There is no friction.
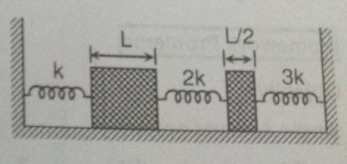
View SolutionThe system shown is figure consists of 3 springs and two rods. If the temperature of the rod is increased by ΔT, then the total energy stored in three springs is β×99484kL2α2(ΔT)2. Determine the value of β. The spring are initially relaxed and there is no friction anywhere. For rod the coefficient of linear expansion is α
_E01_089_Q01.png)
View Solution
Knowledge Check
The moment of ineratia of a uniform thin rod about its perpendicular bisector is I. If the temperature of the rod is increased by Δt , the moment of inertia about perpendicular bisector increases by (coefficient of linear expansion of material of the rod is α).
AZeroBIαΔtC2IαΔtDIαΔt
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beAαA=3×10−6/∘C,500∘CBαA=3×10−6/∘C,222.22∘CCαA=27×10−6/∘C,500∘CDαA=27×10−6/∘C,222.22∘CTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
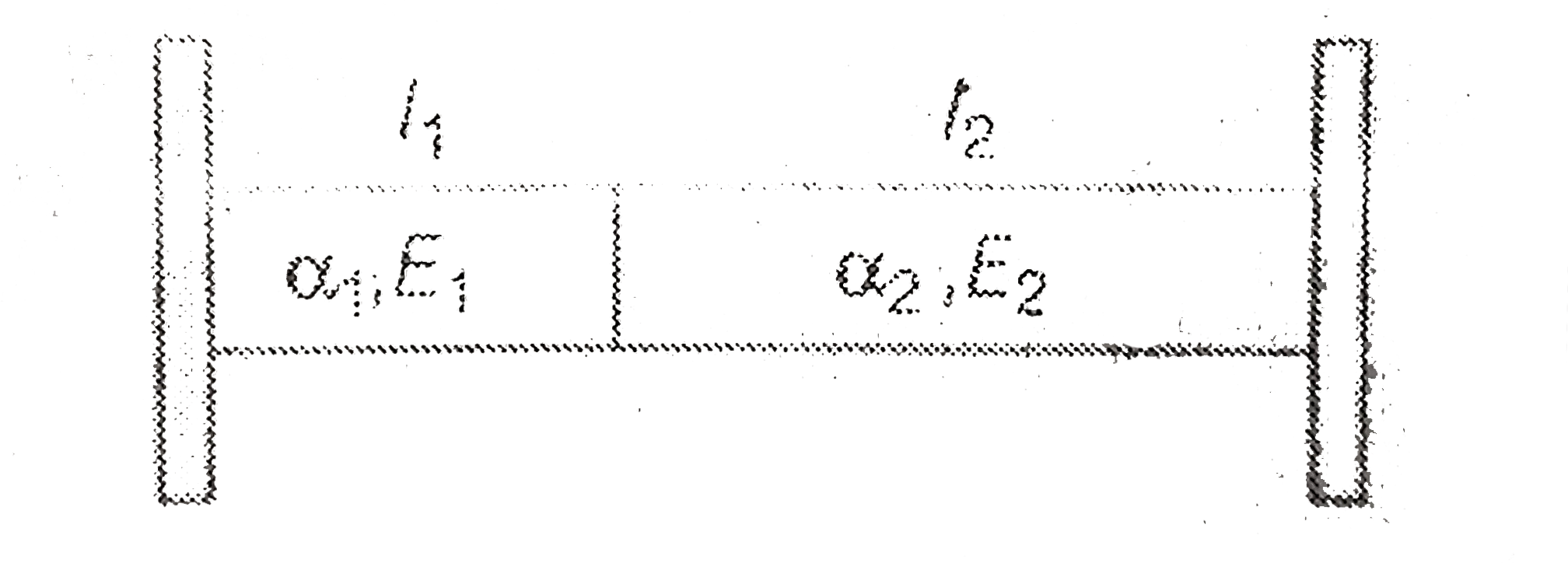 Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2
Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2
The systeam shown is figure consists of 3 springs and two rods. If the temperature of the rod is increased by ΔT, then the total energy stored in three springs is β×99484kL2α2(ΔT)2. Datermine the value of β. The soring are initially relaxed and there is no frication anywhere. For rod the coefficient of linear expansion is α
_E01_089_Q01.png)
View SolutionTwo rods of material X sandwich another rod of material Y as shown in figure. At temperature t, the three rods are in a state of zero strailn and of length L and riveted to each other in this state. If the temperature of the system increases to T+ΔT, find the final length of the system of the three rods. Given that the coefficients of linear expansions of the roods and their Young's modulus for material X and Y are alpnax,αy,Yx and Yy respectively. Consider αy>αx.

View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
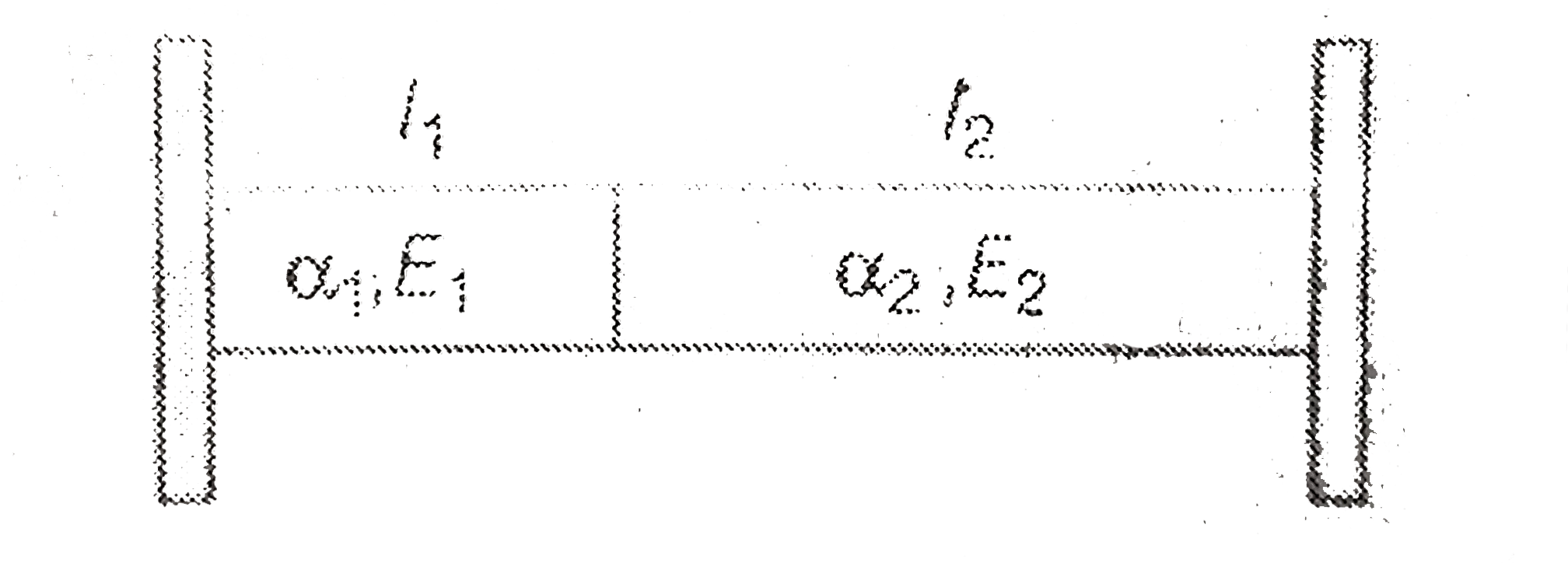
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View Solution

