A slab of uniform cross section is such that , its thermal conductivity K varies with distance x from one ends as . Determine the effective thermal conductivity of the slab .

The entire slab of length l can be subdivided into innumerable elemental section , each of a particular thermal conductivity .
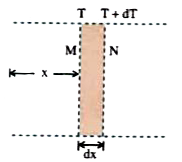
Consider one such section M at distance x from one of the ends X (say) . Let N be another section at a distance x + dx from the end X . Further , let the temperature of the section M and N be T and
Now , thermal current across the section M will be (in steady state).
Now , if be the effective thermal conductivity of the slab , then .
Comparing Eqs. (iv)
[Replacing the summation sign by inergral sign]
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - TEST YOUR SELF6videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS28videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)11videos
THERMOMETRY
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)3videos
TRANSMISSION OF HEAT
Knowledge Check
- Question 1 - Select One
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL - Question 1 - Select One
Three metal rod A, B and C of same length and cross-section are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), then the effective thermal conductivity of the system will be
AKA7B6KB7C7KB3D7KC
Similar Questions
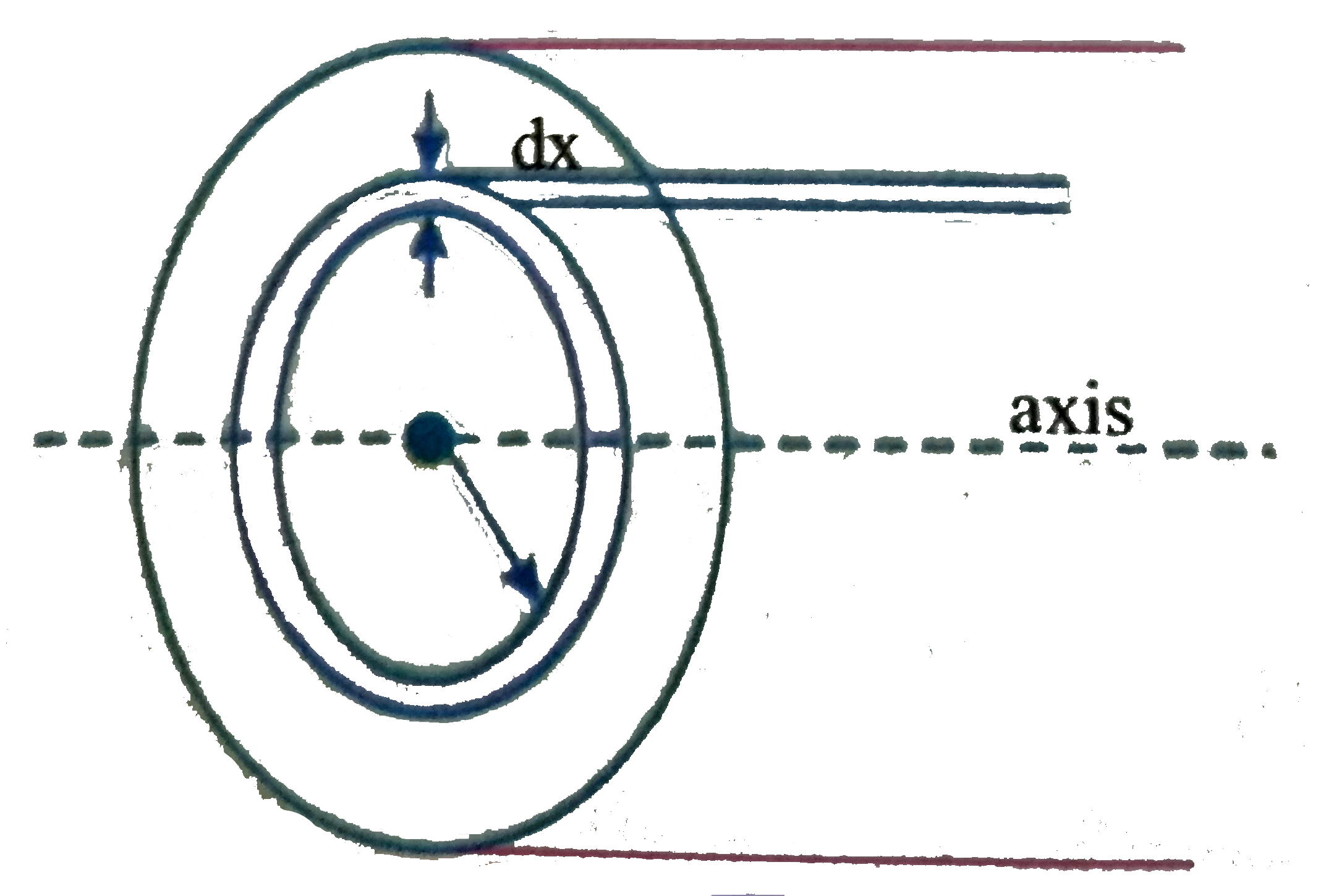
A cylinder of radius R and length l is made uo of a substnace whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2 Detemine the effective thermal conductivity between the flat faces of the cylinder
 .View Solution
.View SolutionA cylinder of radius R and length l is made up of substance whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2. Determine the the effective thermal conductivity between the flat faces of the cylinder.
View SolutionA cylinder of radius R and length l is made up of substance whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2. Determine the the effective thermal conductivity between the flat faces of the cylinder.
View SolutionTwo identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThree identical metal rods A, B and C are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), (KA=49w/mK) calculate the effective thermal conductivity of the system ?
View SolutionThree identical metal rods A, B and C are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is thrice that of C(KC) and half that of A(KA), (KA=49w/mK) calculate the effective thermal conductivity of the system ?
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution

