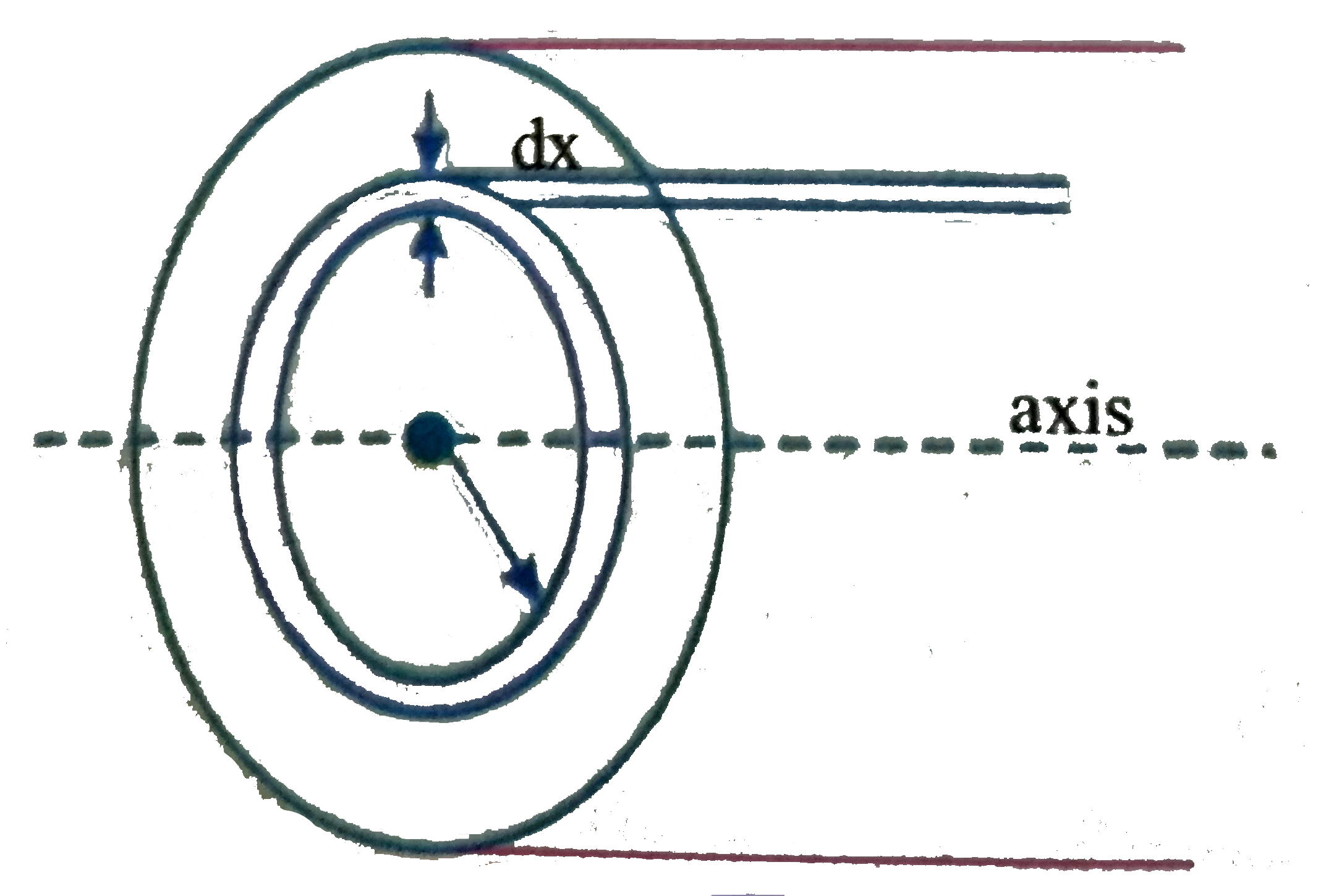
A cylinder of radius R and length l is made uo of a substnace whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2 Detemine the effective thermal conductivity between the flat faces of the cylinder
 .
.
Let us subdivide the entire cylinder into a number of coaxial cylindrical shells of infinitesimally small thickness dx Cross sectional area of the shell is 2πx(dx) Using the experession for the effective thermal conductivity
Keff=∑AiKi∑Ai,Keff=1∑AiR∫0K(2πxdx)
=1πR2R∫0(K1x+K2)2πx(dx)
=2R2R∫0(K1x2+K2x)dx=13(2K1R+3K2) .
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:C .U .Q
Explore 89 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL -1 (C.W)
Explore 1 Video
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
A cylinder of radius R and length l is made up of substance whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2. Determine the the effective thermal conductivity between the flat faces of the cylinder.
View SolutionTwo identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
View Solution
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLIf l is the length, A is the area of cross-section and K the thermal conductivity, then the thermal resistance of the block is given by
AKlABlKACAKlDAKlA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
AK1+K2BK1+8K29CK1K2K1+K2D8K1+K29
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylinderical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effictive thermal conductivity of the system is
View Solution

