A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:

2vsin(2θ)
zero
2vsin(θ2)
2vcos(θ2)
The correct Answer is:C
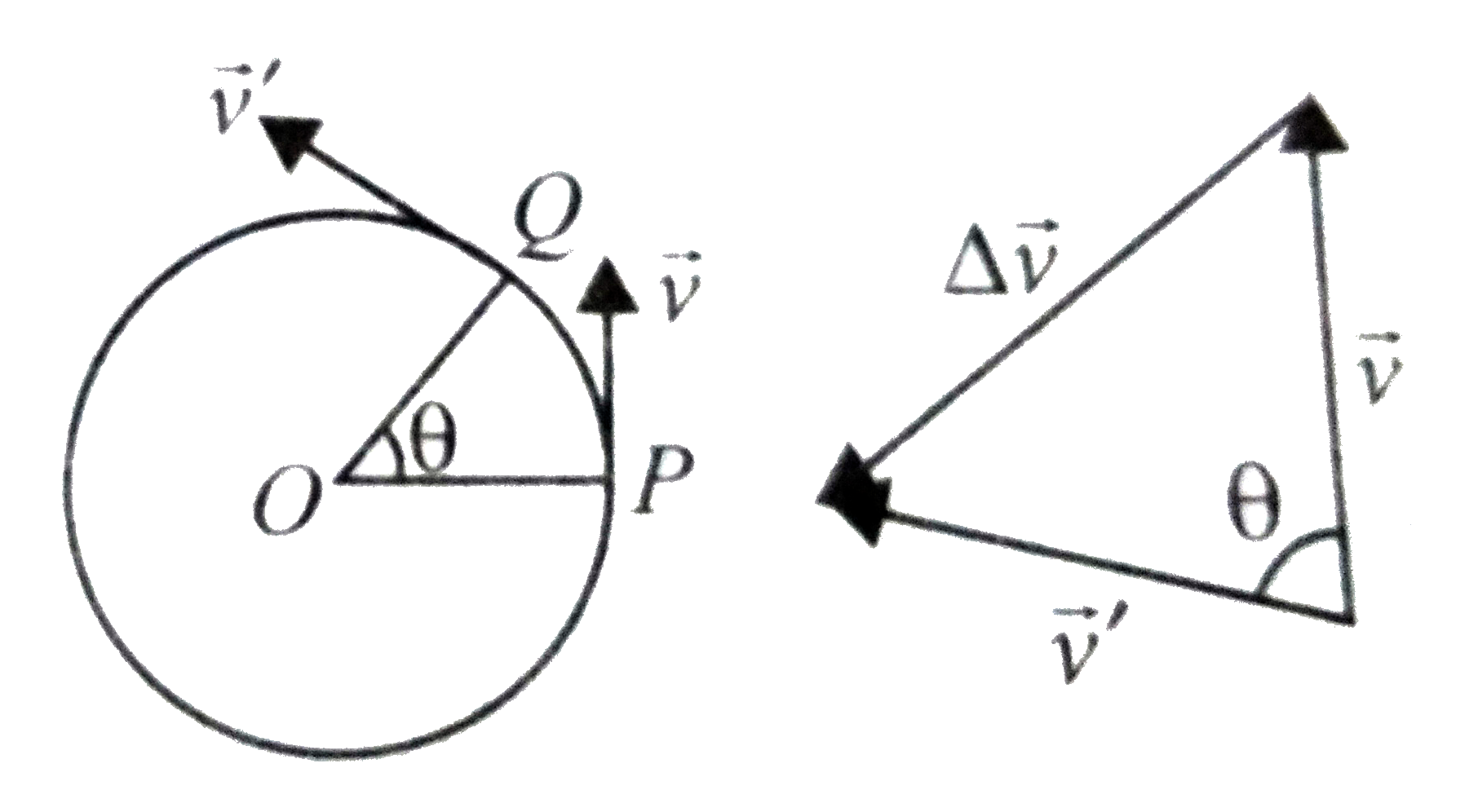
|→v|=|→v|=v
Δ→v=→v−→v
∴|Δ→v|=√v2+v2−2v2cosθ
=√2v2(1−cosθ)=2vsinθ2
Topper's Solved these Questions
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:HOTS
Explore 6 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:EXEMPLER PROBLEMS
Explore 9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assertion And Reason
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:NCERT Exemplar
Explore 6 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle is moving on a circular path with constant speed v then the change in its velocity after it has described an angle of 60∘ will be
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA particle is moving in a circular orbit with constant speed. Select wrong alternate.
View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA particle is moving in a circle of radius r centred at O with constant speed v. What is the change in velocity in moving from AtoB(∠AOB=40∘) ?
View SolutionA particle is moving in a circle of radius r centred at O with constant speed u. What is the change in velocity in moving from AtoB(∠AOB=40∘) ?
View SolutionAn object moving in a circular path at constant speed has constant
View Solution

