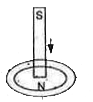
A metal ring is held horizontally and bar magnet is dropped through the ring with its length along the axis of the ring. The acceleration of the falling magnet
equal to g
less than g
more than g
depends of on the diameter of the ring length of magnet
The correct Answer is:B
To solve the problem of the falling bar magnet through a metal ring, we will analyze the situation step by step.
Step 1: Understand the Setup
We have a horizontal metal ring and a bar magnet that is dropped through it. The bar magnet has its length aligned with the axis of the ring.
Hint: Visualize the scenario by drawing a diagram of the ring and the magnet to understand their positions relative to each other.
Step 2: Identify the Motion of the Magnet
As the bar magnet falls through the ring, it experiences a gravitational force acting downwards. This force is equal to the weight of the magnet, which is given by F=mg, where m is the mass of the magnet and g is the acceleration due to gravity.
Hint: Remember that the magnet is subject to gravitational force, but we need to consider other forces acting on it as well.
Step 3: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's law, a changing magnetic field through the ring will induce an electromotive force (emf) in the ring. As the magnet falls, the magnetic field around the ring changes, leading to the induction of a current in the ring.
Hint: Recall that the direction of the induced current can be determined using Lenz's law, which states that the induced current will flow in a direction that opposes the change in magnetic flux.
Step 4: Determine the Direction of Induced Current
When the north pole of the magnet approaches the ring, the induced current will flow in such a way as to create a north pole at the side of the ring facing the magnet. This induced north pole will repel the north pole of the falling magnet, thus opposing its motion.
Hint: Think about how the poles of magnets interact. Like poles repel and unlike poles attract.
Step 5: Analyze the Effect on the Magnet's Acceleration
Since the induced current opposes the motion of the falling magnet, it will experience a magnetic force acting upwards, which reduces its acceleration. Therefore, the net acceleration of the magnet will be less than g.
Hint: Consider the forces acting on the magnet: the gravitational force downwards and the magnetic force upwards due to the induced current.
Step 6: Conclusion
The acceleration of the falling magnet is less than the acceleration due to gravity (g). Thus, we conclude that the answer to the question is that the acceleration of the falling magnet is less than g.
Final Answer: The acceleration of the falling magnet is less than g.
We have a horizontal metal ring and a bar magnet that is dropped through it. The bar magnet has its length aligned with the axis of the ring.
As the bar magnet falls through the ring, it experiences a gravitational force acting downwards. This force is equal to the weight of the magnet, which is given by F=mg, where m is the mass of the magnet and g is the acceleration due to gravity.
According to Faraday's law, a changing magnetic field through the ring will induce an electromotive force (emf) in the ring. As the magnet falls, the magnetic field around the ring changes, leading to the induction of a current in the ring.
When the north pole of the magnet approaches the ring, the induced current will flow in such a way as to create a north pole at the side of the ring facing the magnet. This induced north pole will repel the north pole of the falling magnet, thus opposing its motion.
Since the induced current opposes the motion of the falling magnet, it will experience a magnetic force acting upwards, which reduces its acceleration. Therefore, the net acceleration of the magnet will be less than g.
The acceleration of the falling magnet is less than the acceleration due to gravity (g). Thus, we conclude that the answer to the question is that the acceleration of the falling magnet is less than g.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:EXEMPLAR PROBLEMS
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSERTION AND REASON
Explore 15 Videos
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTPS ENGLISHChapter:ELECTRIC CHARGES AND FIELDSExercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A closed iron ring is held horizontally and a bar magnet is dropped through the ring with its length along the axis of he ring. The acceleration of the falling is
View SolutionConsider metal ring kept on a horizontal plane . A bar magnet is held above the ring with its length along the axis is held above the ring with its length along the axis of the ring . If the magnet is dropped freely the acceleration of the falling magnet is : ( g is accelration due to gravity )
View SolutionA metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
View SolutionA bar magnet is dropped along the axis of copper ring held horizontally. The acceleration of fall is
View SolutionA resistance coil is held horizontally and a magnet is allowed to fall vertically through it . Then the acceleration of the magnet while passing through the coil is
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionIn the figure shown, the magnet is pushed towards the fixed ring along the axis of the ring and it passes through the ring.
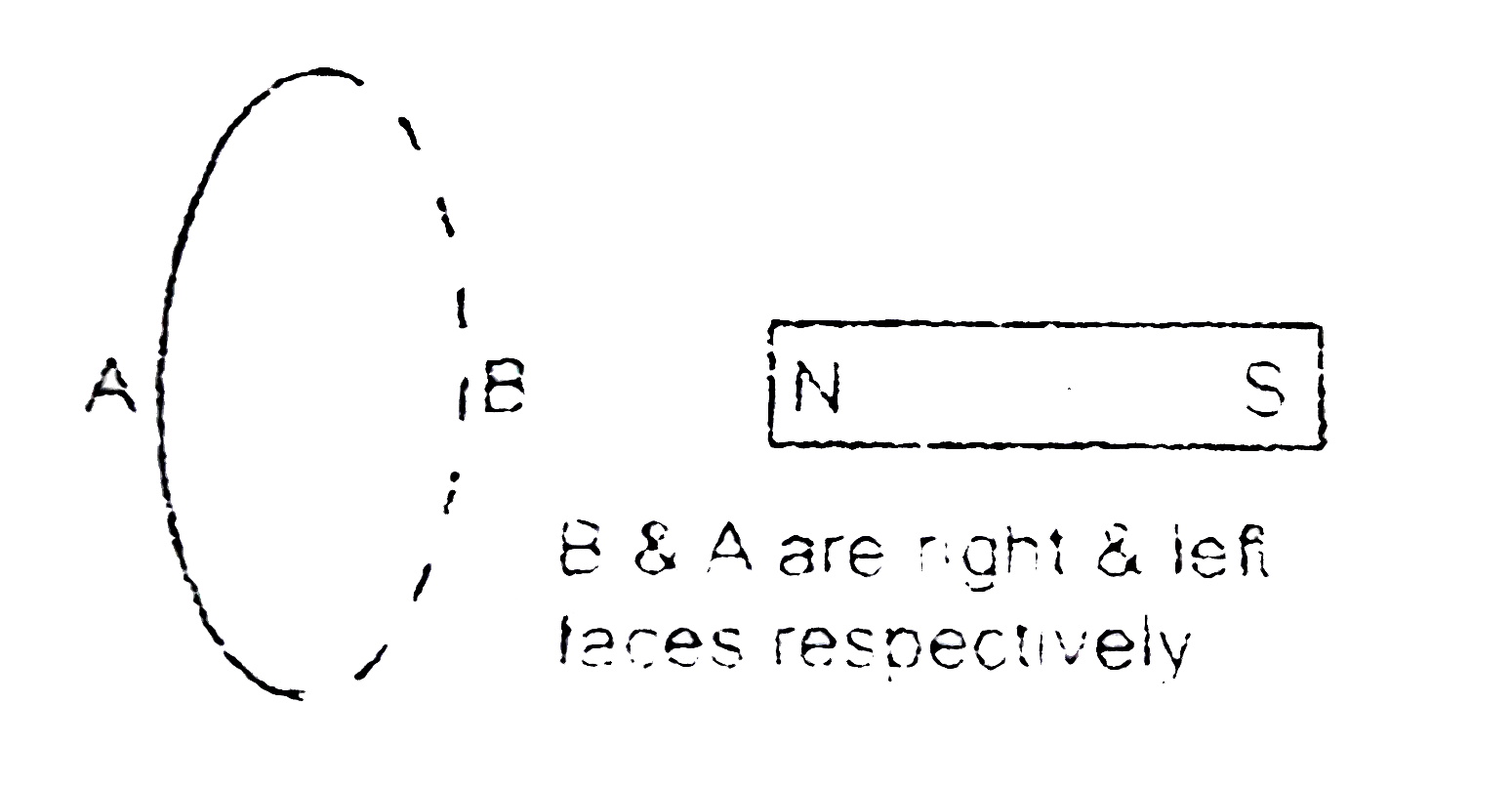
View SolutionA bar magnet is dropped through a horizontal aluminium ring along the axis of the ring. What will be direction of induced current in the loop for the observer shown? What will be the direction of magnetic force experienced by the bar magnet?

View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,

View Solution

