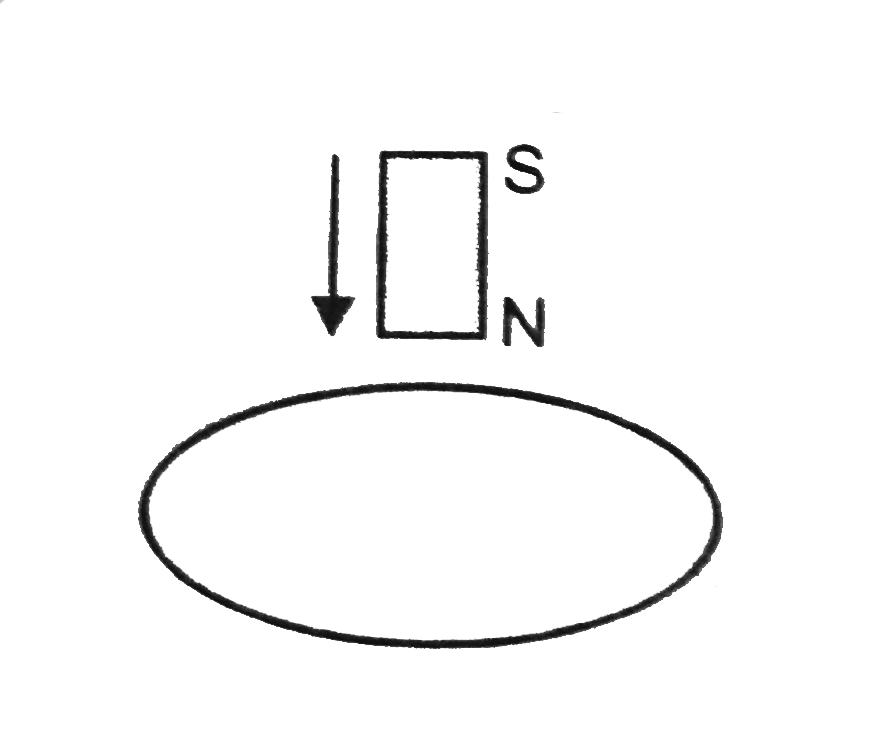
A bar magnet is dropped along the axis of copper ring held horizontally. The acceleration of fall is
equal to the acceleration due to gravity at that place
less than the acceleration due to gravity at that place
greater than the acceleration due to gravity at that place
twice the acceleration due to gravity at that place
The correct Answer is:B
To solve the problem of a bar magnet being dropped along the axis of a copper ring held horizontally, we can follow these steps:
Step 1: Understand the Setup
We have a bar magnet and a copper ring. The bar magnet is dropped vertically through the center of the copper ring.
Hint: Visualize the setup to understand the interaction between the magnet and the ring.
Step 2: Identify the Magnetic Field Changes
As the bar magnet falls, it creates a changing magnetic field in the vicinity of the copper ring. The magnetic field lines of the magnet will change as it moves, leading to a change in magnetic flux through the ring.
Hint: Remember that a changing magnetic field can induce an electromotive force (EMF) in a conductor.
Step 3: Apply Faraday’s Law of Electromagnetic Induction
According to Faraday's law, the induced EMF (ε) in the ring is proportional to the rate of change of magnetic flux (Φ) through the ring:
ϵ=−dΦdt
Where Φ is the magnetic flux given by:
Φ=B⋅A
Here, B is the magnetic field due to the bar magnet, and A is the area of the ring.
Hint: Consider how the magnetic flux changes as the magnet falls.
Step 4: Induced Current and Magnetic Field
The induced EMF will cause a current to flow in the copper ring. According to Lenz's law, the direction of this induced current will be such that it opposes the change in magnetic flux that produced it. This means that the current will create a magnetic field that opposes the magnetic field of the falling magnet.
Hint: Think about how the induced current interacts with the magnetic field of the falling magnet.
Step 5: Effect on the Acceleration of the Magnet
Due to the opposing magnetic field created by the induced current in the ring, the bar magnet will experience a magnetic force that opposes its motion. This results in a reduction of the acceleration of the falling magnet. Instead of falling freely under gravity (g), the magnet will fall with an acceleration less than g.
Hint: Remember that the net force acting on the magnet will be less than its weight due to the opposing magnetic force.
Step 6: Conclusion
The final conclusion is that the acceleration of the falling bar magnet is less than the acceleration due to gravity (g). Therefore, the answer to the question is that the acceleration of fall is less than g.
Final Answer: The acceleration of the fall is less than g.
We have a bar magnet and a copper ring. The bar magnet is dropped vertically through the center of the copper ring.
As the bar magnet falls, it creates a changing magnetic field in the vicinity of the copper ring. The magnetic field lines of the magnet will change as it moves, leading to a change in magnetic flux through the ring.
According to Faraday's law, the induced EMF (ε) in the ring is proportional to the rate of change of magnetic flux (Φ) through the ring:
ϵ=−dΦdt
Where Φ is the magnetic flux given by:
Φ=B⋅A
Here, B is the magnetic field due to the bar magnet, and A is the area of the ring.
The induced EMF will cause a current to flow in the copper ring. According to Lenz's law, the direction of this induced current will be such that it opposes the change in magnetic flux that produced it. This means that the current will create a magnetic field that opposes the magnetic field of the falling magnet.
Due to the opposing magnetic field created by the induced current in the ring, the bar magnet will experience a magnetic force that opposes its motion. This results in a reduction of the acceleration of the falling magnet. Instead of falling freely under gravity (g), the magnet will fall with an acceleration less than g.
The final conclusion is that the acceleration of the falling bar magnet is less than the acceleration due to gravity (g). Therefore, the answer to the question is that the acceleration of fall is less than g.
Similar Questions
A bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionA closed iron ring is held horizontally and a bar magnet is dropped through the ring with its length along the axis of he ring. The acceleration of the falling is
View Solution
Knowledge Check
A metal ring is held horizontally and bar magnet is dropped through the ring with its length along the axis of the ring. The acceleration of the falling magnet
Aequal to gBless than gCmore than gDdepends of on the diameter of the ring length of magnet
Assertion. The bar magnet falling vertically along the axis of the horizontal coil will be having acceleartion less than g.
Resaon. Clockwise current induced in the coil.
View SolutionAssertion A magnetic is dropped along the axis of a circular conducting loop as shown in figure. Then, acceleration of magnet is always less than g.
Reason When magnet is above the loop, then it will repel the magnet and when it is below the loop, then it will attract the magnet.

View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionConsider metal ring kept on a horizontal plane . A bar magnet is held above the ring with its length along the axis is held above the ring with its length along the axis of the ring . If the magnet is dropped freely the acceleration of the falling magnet is : ( g is accelration due to gravity )
View SolutionA magnet is allowed to fall towards a metal ring. During the fall Its accelertion is
View SolutionA metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
View SolutionA short magnet is allowed to fall from rest along the axis of a horizontal conducting ring. The distance fallen by the magnet in one second may be
View Solution

