A charged particle having drift velocity of in electric field of mobility is
The correct Answer is:B
To find the mobility of a charged particle given its drift velocity and the electric field, we can follow these steps:
1. Identify the given values:
- Drift velocity (Vd) = 7.5×10−4m/s
- Electric field (E) = 3×10−10V/m
2. Recall the formula for mobility (μ):
- Mobility is defined as the ratio of drift velocity to the electric field:
μ=VdE
3. Substitute the given values into the formula:
μ=7.5×10−4m/s3×10−10V/m
4. Perform the division:
- First, divide the coefficients:
7.53=2.5
- Next, handle the powers of ten:
10−410−10=10−4−(−10)=10−4+10=106
- Therefore, combining these results:
μ=2.5×106m2/V s
5. Write the final answer with the appropriate units:
- The mobility of the charged particle is:
μ=2.5×106m2/V s
- Drift velocity (Vd) = 7.5×10−4m/s
- Electric field (E) = 3×10−10V/m
- Mobility is defined as the ratio of drift velocity to the electric field:
μ=VdE
μ=7.5×10−4m/s3×10−10V/m
- First, divide the coefficients:
7.53=2.5
- Next, handle the powers of ten:
10−410−10=10−4−(−10)=10−4+10=106
- Therefore, combining these results:
μ=2.5×106m2/V s
- The mobility of the charged particle is:
μ=2.5×106m2/V s
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - LIMITATIONS OF OHM S LAW4videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - RESISTIVITY7videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - OHM S LAW7videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason30videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
A charged particle having drift velocity of 7.5 x 10−4ms in an electric field of 3 x 10−10Vm has a mobility in m2V−1s−1
View SolutionA charged particle of radius 5×10−7m is located in a horizontal electric field of intensity 6.28×105Vm−1. The surrounding medium has the coeffecient of viscosity η=1.6×10−5Nsm−2. The particle starts moving under the effect of electric field and finally attains a uniform horizontal speed of 0.02ms−1. Find the number of electrons on it. Assume gravity free space.
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 10−3kg and charge 5μC is thrown at a speed of 20ms−1 against a uniform electric field of strength 2×105NC−1. The distance travelled by particle before coming to rest is
A0.1 mB0.2 mC0.3 mD0.4 m - Question 2 - Select One
An electron is moving in a cyclotron at a speed of 3.2×107ms−1 in a magnetic field of 5×10−4T perpendicular to it. What is the frequency of this electron? (q=1.6×10−19C,mc=9.1×10−31kg)
A1.4×105HzB1.4×107HzC1.4×106HzD1.4×109Hz
A charged particle with a velocity 2×103ms−1 passes undeflected through electric field and magnetic fields in mutually perpendicular directions. The magnetic field is 1.5 T. the magnitude of electric field will be
View SolutionAn electron entering field normally with a velocity 4×107ms−1 travels a distance of 0.10 m in an electric field of intensity 3200Vm−1. What is the deviation from its path?
View SolutionElectrons having a velocity →v of 2×106ms−1 pass undeviated through a uniform electric field →E of intensity 5×104Vm−1 and a uniform magnetic field →B.
(i) Find the magnitude of magnetic flux density B of the magnetic field.
(ii) What is the direction of →B, if →v is towards right and →E is vertically downwards in the plane of this paper ?View Solution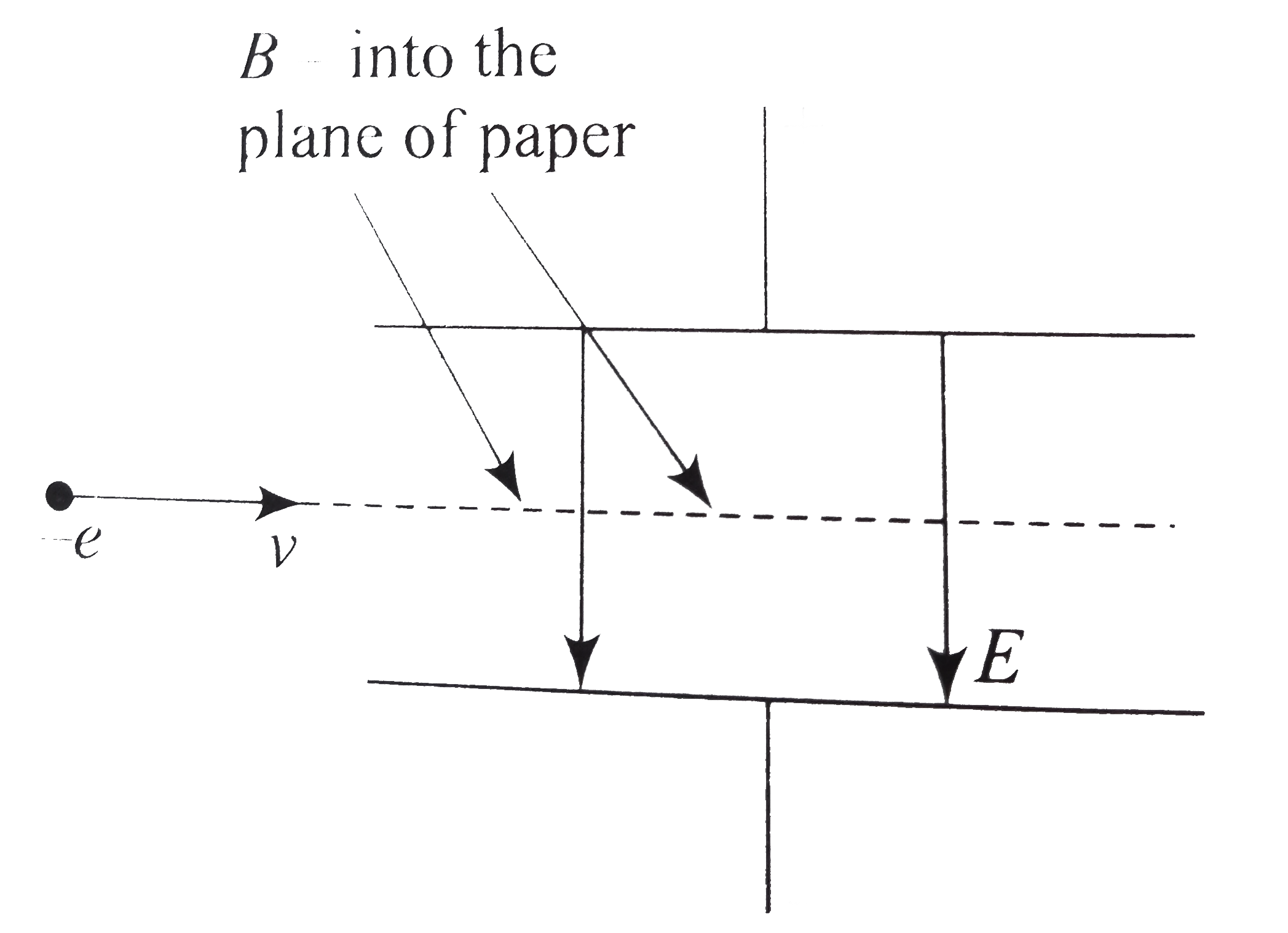
Electrons taveling at a velocity of 2.4×106ms−1 enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is 3.0×106 Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields willView SolutionA particle of charge −16×10−18 coo–mb moving with velocity 10ms−1 along the x−aξs, and an electric field of magnitude (104)/(m) is along the negative z−ais. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View Solution
