Electrons having a velocity of pass undeviated through a uniform electric field of intensity and a uniform magnetic field .
(i) Find the magnitude of magnetic flux density B of the magnetic field.
(ii) What is the direction of , if is towards right and is vertically downwards in the plane of this paper ?
To solve the problem, we will follow these steps:
Step 1: Write down the given values
- Velocity of electrons, v=2×106m/s
- Electric field intensity, E=5×104V/m
Step 2: Use the formula for the relationship between electric field, magnetic field, and velocity
When electrons pass undeviated through both electric and magnetic fields, the electric force is balanced by the magnetic force. The relationship can be expressed as:
E=vB
Where:
- E is the electric field intensity,
- v is the velocity of the electrons,
- B is the magnetic flux density.
Step 3: Rearrange the formula to solve for B
We can rearrange the formula to find B:
B=Ev
Step 4: Substitute the known values into the equation
Substituting the values of E and v:
B=5×104V/m2×106m/s
Step 5: Calculate the value of B
Now we perform the calculation:
B=5×1042×106=52×10−2=2.5×10−2T
Step 6: Determine the direction of the magnetic field →B
To find the direction of →B, we can use the right-hand rule. Given:
- The velocity →v is towards the right,
- The electric field →E is vertically downwards.
Using the right-hand rule:
1. Point your fingers in the direction of →v (to the right).
2. Curl your fingers downwards in the direction of →E.
3. Your thumb will point in the direction of →B.
Since the velocity is to the right and the electric field is downwards, the thumb will point into the plane of the paper.
Final Answers
(i) The magnitude of the magnetic flux density B is 2.5×10−2T.
(ii) The direction of →B is into the plane of the paper.
- Velocity of electrons, v=2×106m/s
- Electric field intensity, E=5×104V/m
When electrons pass undeviated through both electric and magnetic fields, the electric force is balanced by the magnetic force. The relationship can be expressed as:
- E is the electric field intensity,
- v is the velocity of the electrons,
- B is the magnetic flux density.
We can rearrange the formula to find B:
Substituting the values of E and v:
Now we perform the calculation:
To find the direction of →B, we can use the right-hand rule. Given:
- The velocity →v is towards the right,
- The electric field →E is vertically downwards.
1. Point your fingers in the direction of →v (to the right).
2. Curl your fingers downwards in the direction of →E.
3. Your thumb will point in the direction of →B.
(i) The magnitude of the magnetic flux density B is 2.5×10−2T.
Similar Questions
A charged particle with a velocity 2×103ms−1 passes undeflected through electric field and magnetic fields in mutually perpendicular directions. The magnetic field is 1.5 T. the magnitude of electric field will be
View Solution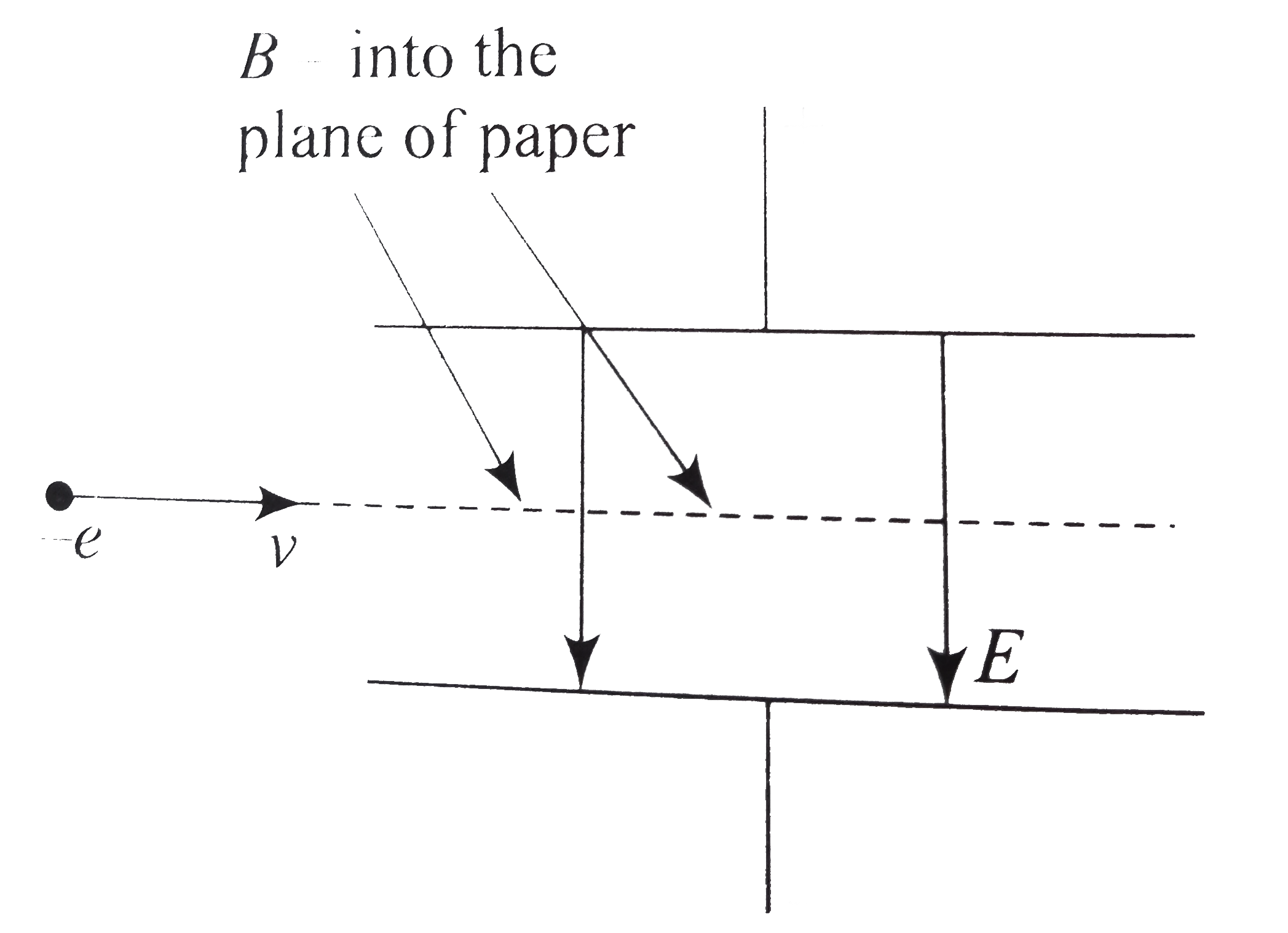
Electrons taveling at a velocity of 2.4×106ms−1 enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is 3.0×106 Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields will
View SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View SolutionAn electron entering field normally with a velocity 4×107ms−1 travels a distance of 0.10 m in an electric field of intensity 3200Vm−1. What is the deviation from its path?
View SolutionThe magnitude of earth magnetic field at magnetic equator is 2.8×10−5T . Find magnitude of earth's magnetic field near geomagnetic poles .
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionA rectangular coil having 60 turns and area of 0.4 m2 is held at right angles to a uniform magnetic field of flux density 5×10−5T. Calculate the magnetic flux passing through it.
View Solution
