An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
te=√2Sae=√2smeeE
=√2×1.5×10−2×9.1×10−311.6×10−19×2×104
=2.9×10−9s
tp=√2sap=√2smPeE
=√2×1.5×1−2×1.67×10−271.6×10−19×2×104
=1.3×107s
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question45videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTION( ONLY ONE ANSWER)12videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)15videos
ELECTROMAGNETIC INDUCTION
Similar Questions
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
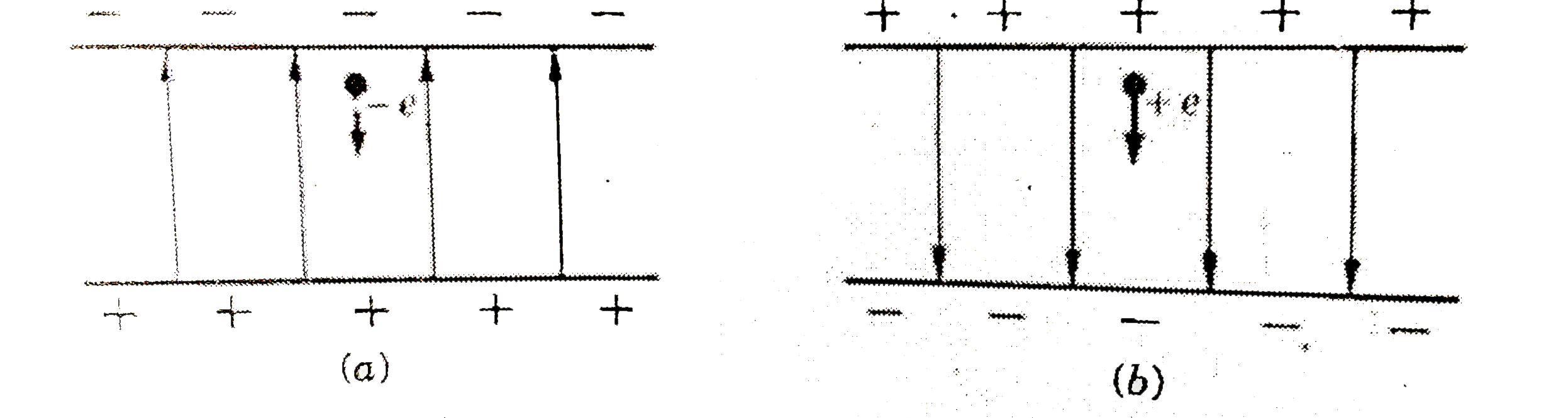 View Solution
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
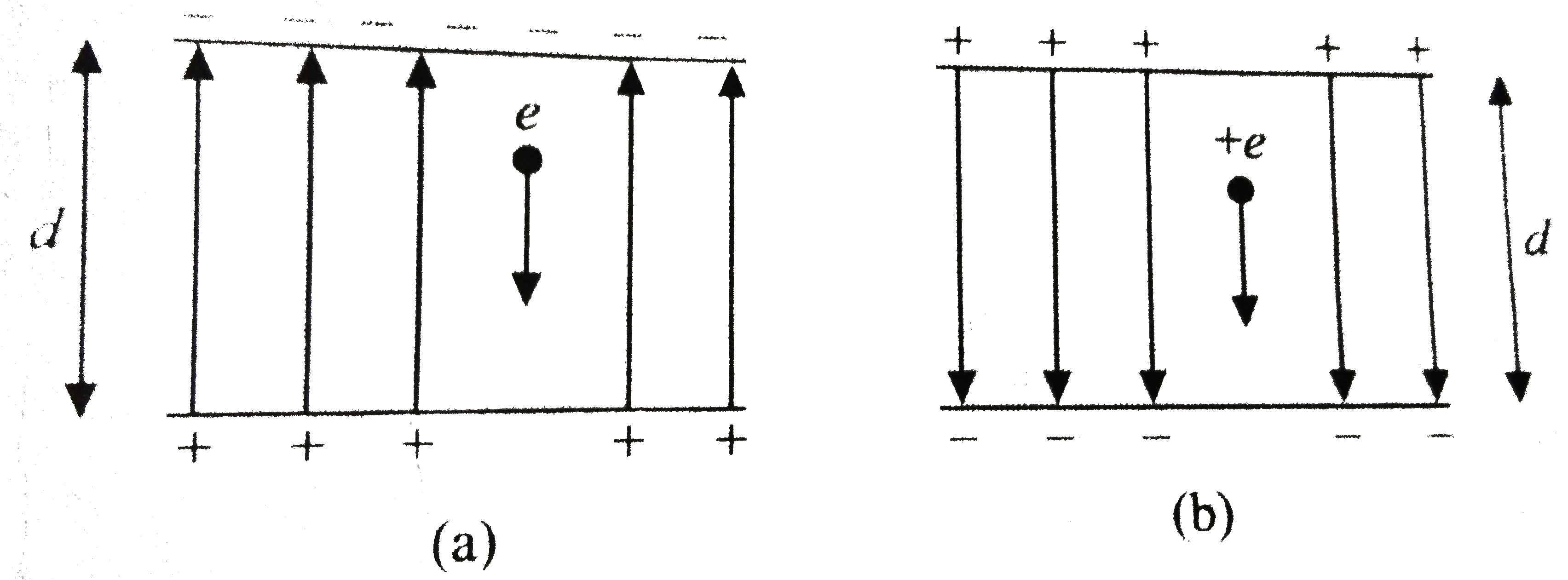 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View SolutionAn electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
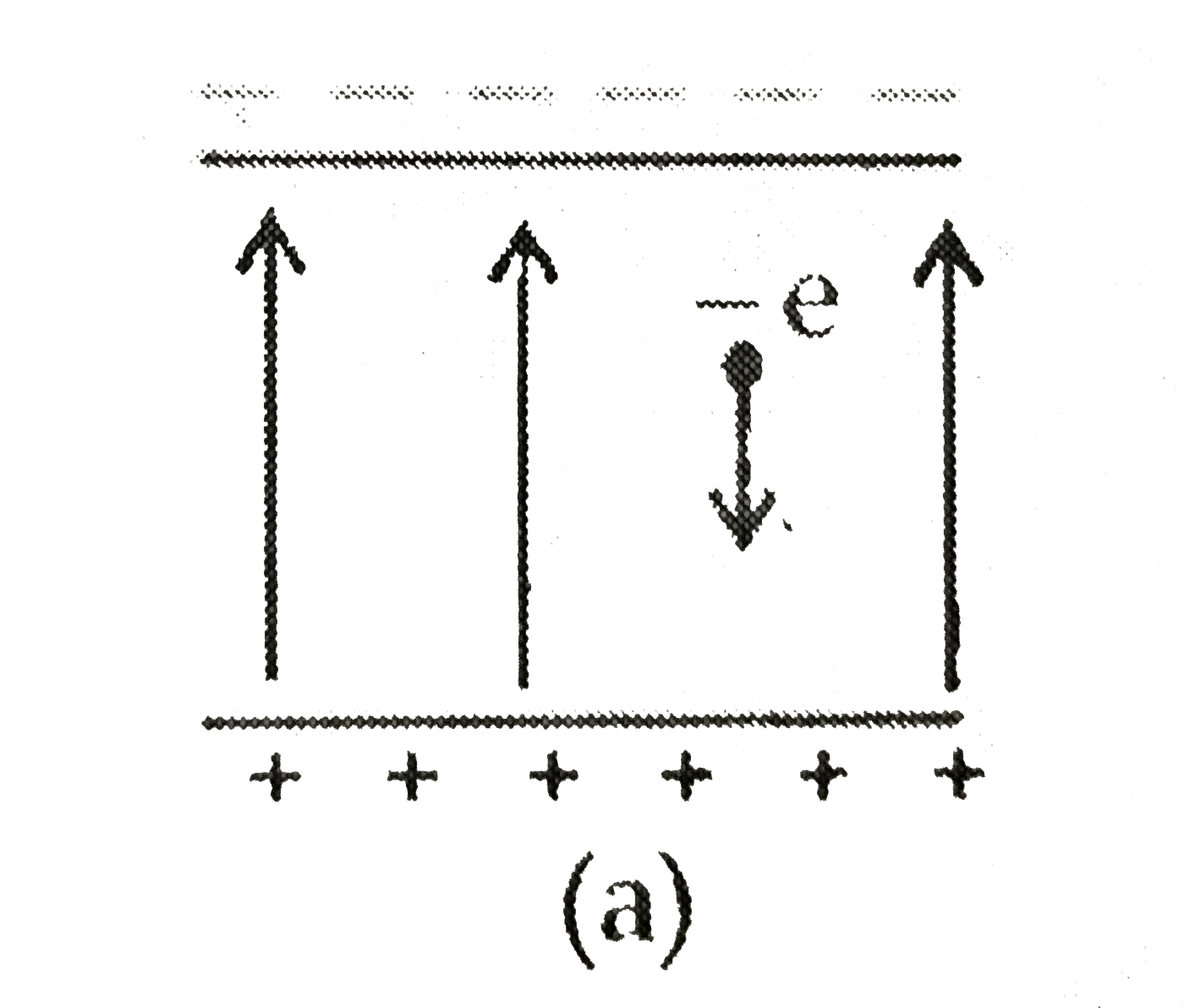
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.
 View Solution
View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
View SolutionCalculate the total electric flux through the paraboloidal surface due to a uniform electric field of magnitude E0 in the direction shown in figure.
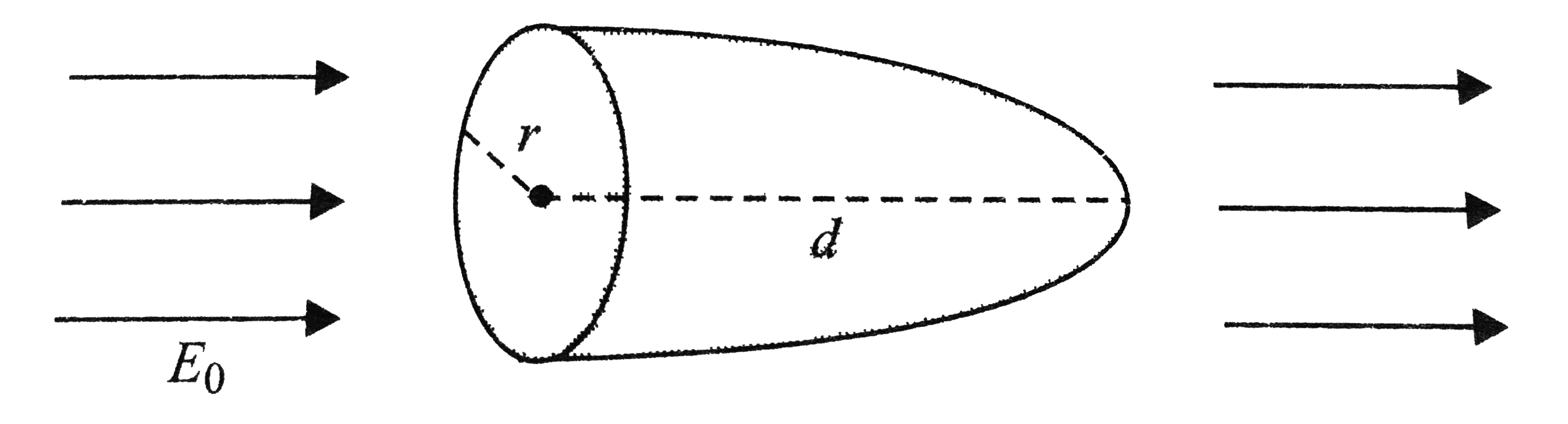 View Solution
View SolutionAn electron accelerated through 500 V , enters a transverse uniform magnetic field of magnitude 100 mT . The radius of the circular path described by the electron is nearly
View SolutionA circular plane sheet of radius 10 cm is placed in a uniform electric field of 5×105NC−1, making an angle of 60∘ with the field. Calculate electric flux through the sheet.
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View Solution


