An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
1.3×102s
2.1×10−12s
1.6×10−10s
2.9×10−9s
The correct Answer is:D
Here, the direction of field is upward,
So the negatively charged electron experiences a dowanward force.
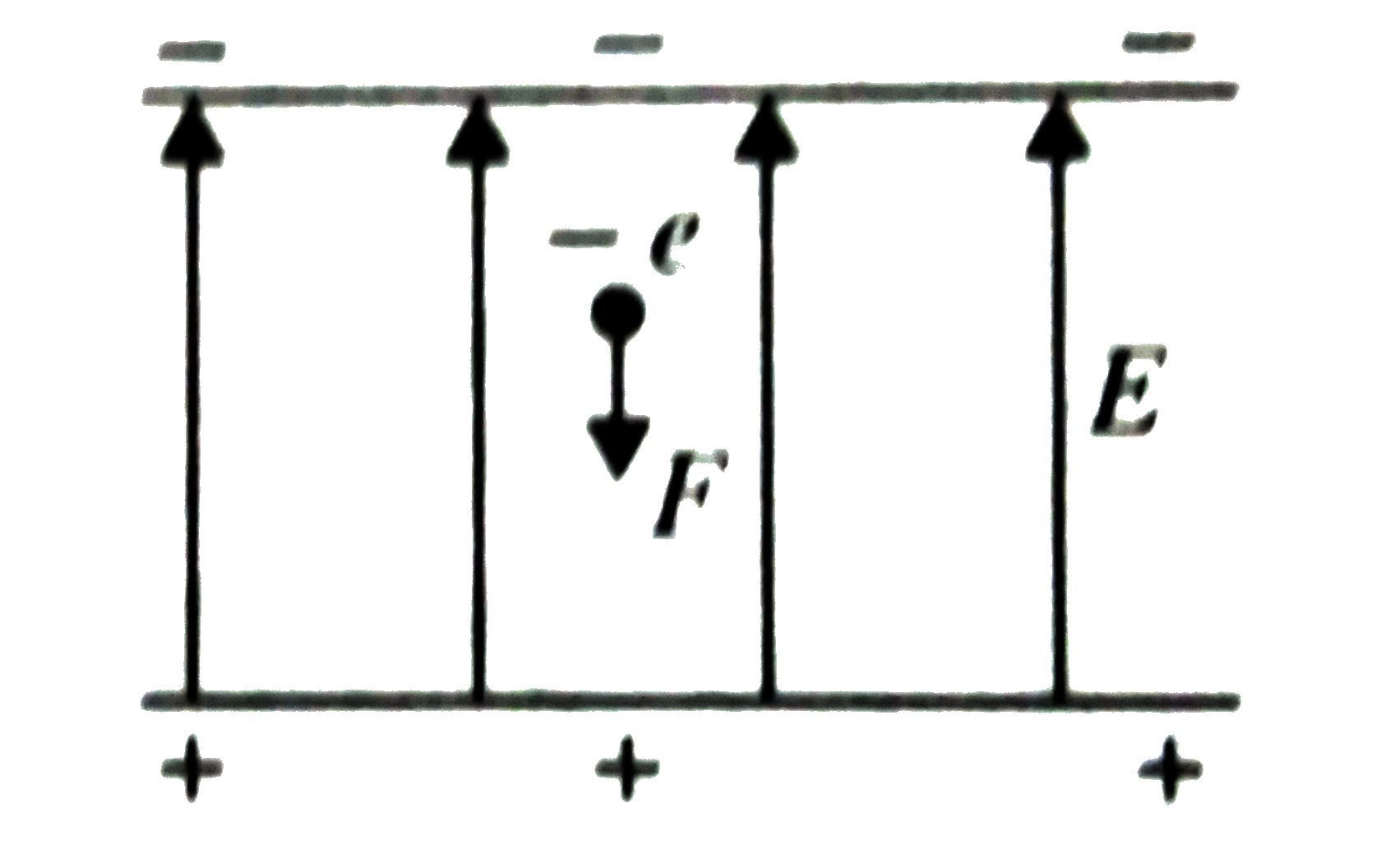
∴ The acceleration of electron is
ae=eEme
The time required by the electron to fall through a distance h is
te=√(2hae)=√2hmeeE
=[2×1.5×10−2×9.11×10−311.6×10−19×2×104]1/2=2.9×10−9s
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - ASSERTION & REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Electric Charges
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
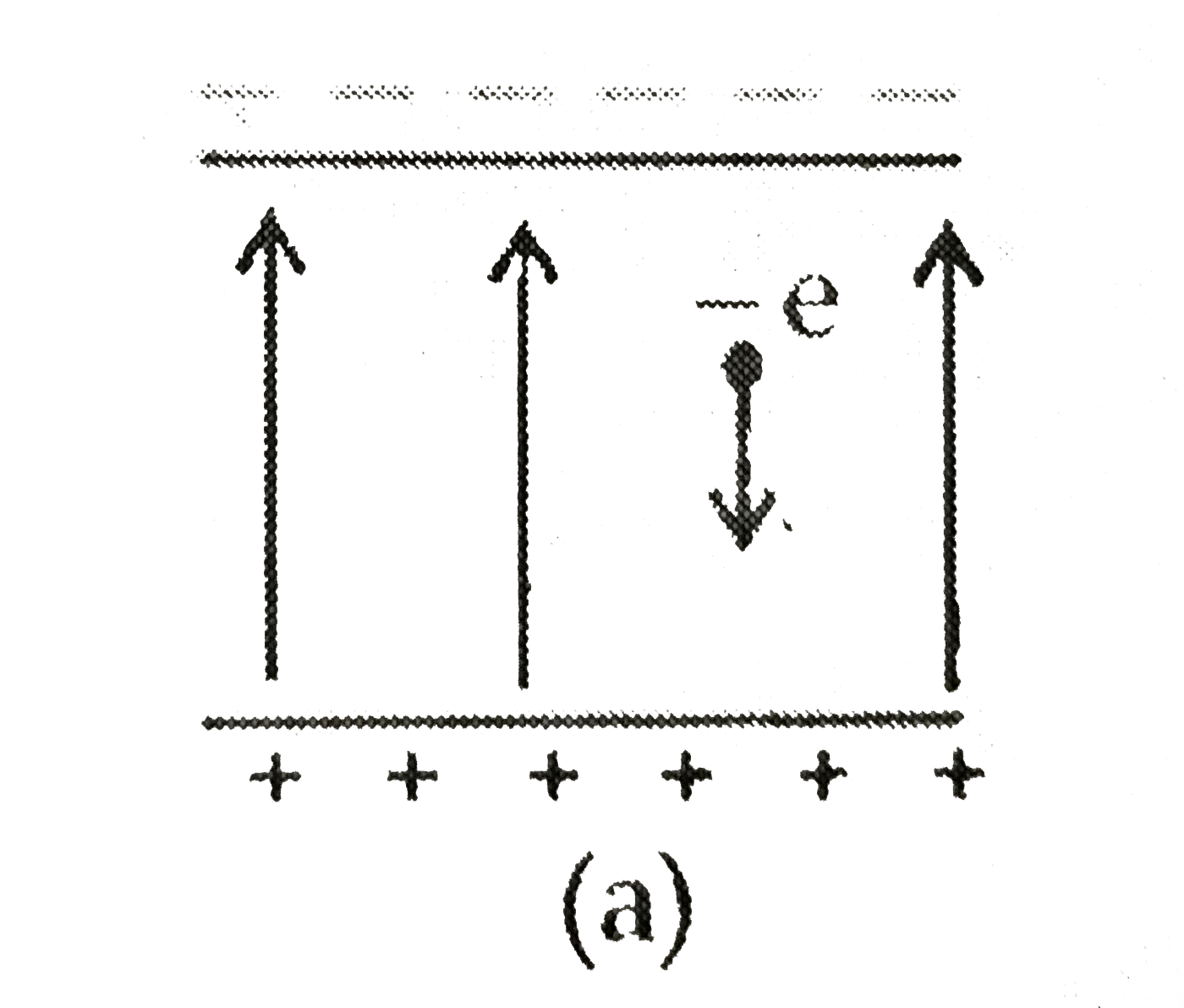
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
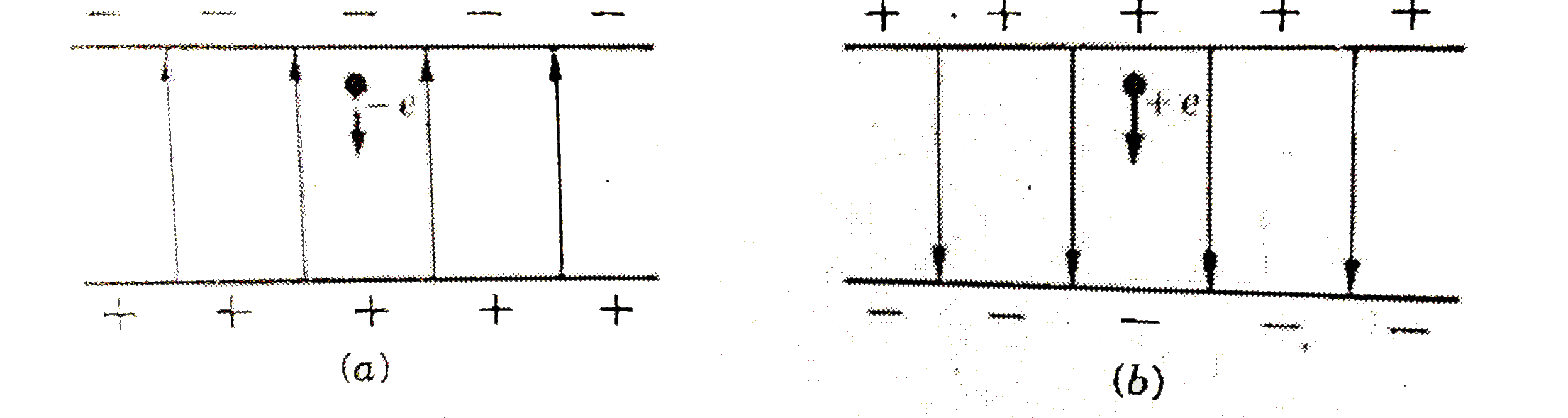
View Solution
Knowledge Check
An electron of mass Me, initially at rest, moves through a certain distance in a uniform electric field in time t1. A proton of mass Mp also initially at rest, takes time t2 to move through an equal distance in this uniform electric field. Neglecting the effect of gravity, the ratio t2/t1 is nearly equal to
A(mpme)1/2B(memp)1/2C1D1836
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
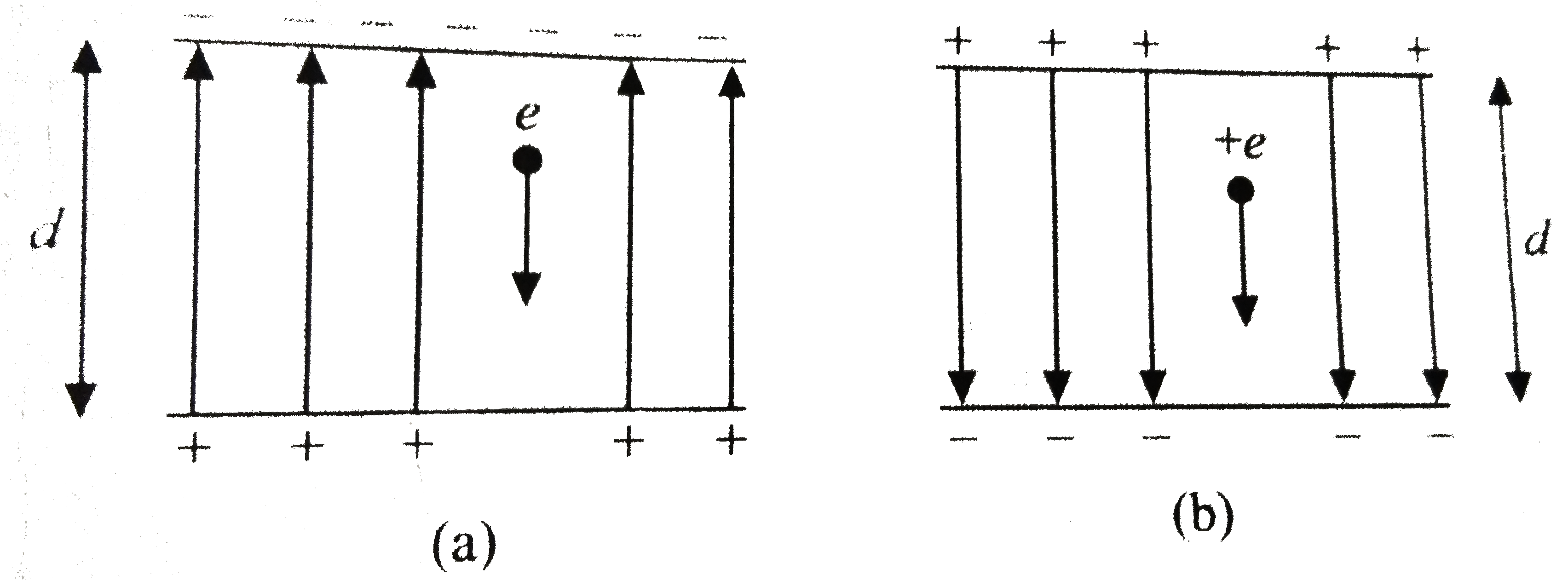 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn electron (q=1.6×10−19C) is moving at right angles to a uniform magnetic field of 3.534×10−5 T The time taken by the electron to complete a circular orbit is
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View Solution
