Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
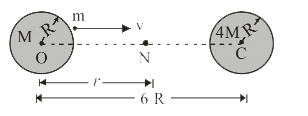
√45GMR
√54GMR
√35GMR
√53GMR
The correct Answer is:C
( c) 
Let the projectile of mass m be fired with minimum velocity, v from the surface of sphere of mass M to reach the surface of sphere of mass 4M. Let N be neutral point at a distance r from the centre of the sphere of mass M. At neutral point N,
GMmr2=G(4M)m(6R−r)2
(6R−r)2=4r2
6R−r=±2rorr=2Ror−6R
The point r= -6R does not conern us. Thus, ON=r=2R
It is sufficient to project the projectile with a speed which would enable it to reach N. Thereafter, the greater gravitational pull of 4M would suffice.
The mechanical energy at the surface of M is
Ei=12mv2−GMmR−G(4M)m5R
AT the neutral point, N the speed approaches zero.
∴ The mechanical enery at N is
EN=−GMm2R−G(4M)m4R=−GMm2R−GMmR
According to law of conservation of mechanical energy,
Ei=EN
1P2mv2−GMmR−4GMm5R=−GMm2R−GMmR
v2f=2GMR[45−12]=35GMRorv=(35GMR)1/2
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Earth Satellite
4 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Energy of an Orbiting Satellite
15 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Gravitational Potential energy
7 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of massm is projected from the surface of the sphere of mass M directly towards the centre of teh second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View Solution
Knowledge Check
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
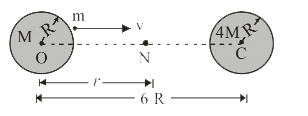 A√45GMRB√54GMRC√35GMRD√53GMR
A√45GMRB√54GMRC√35GMRD√53GMR
Two solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
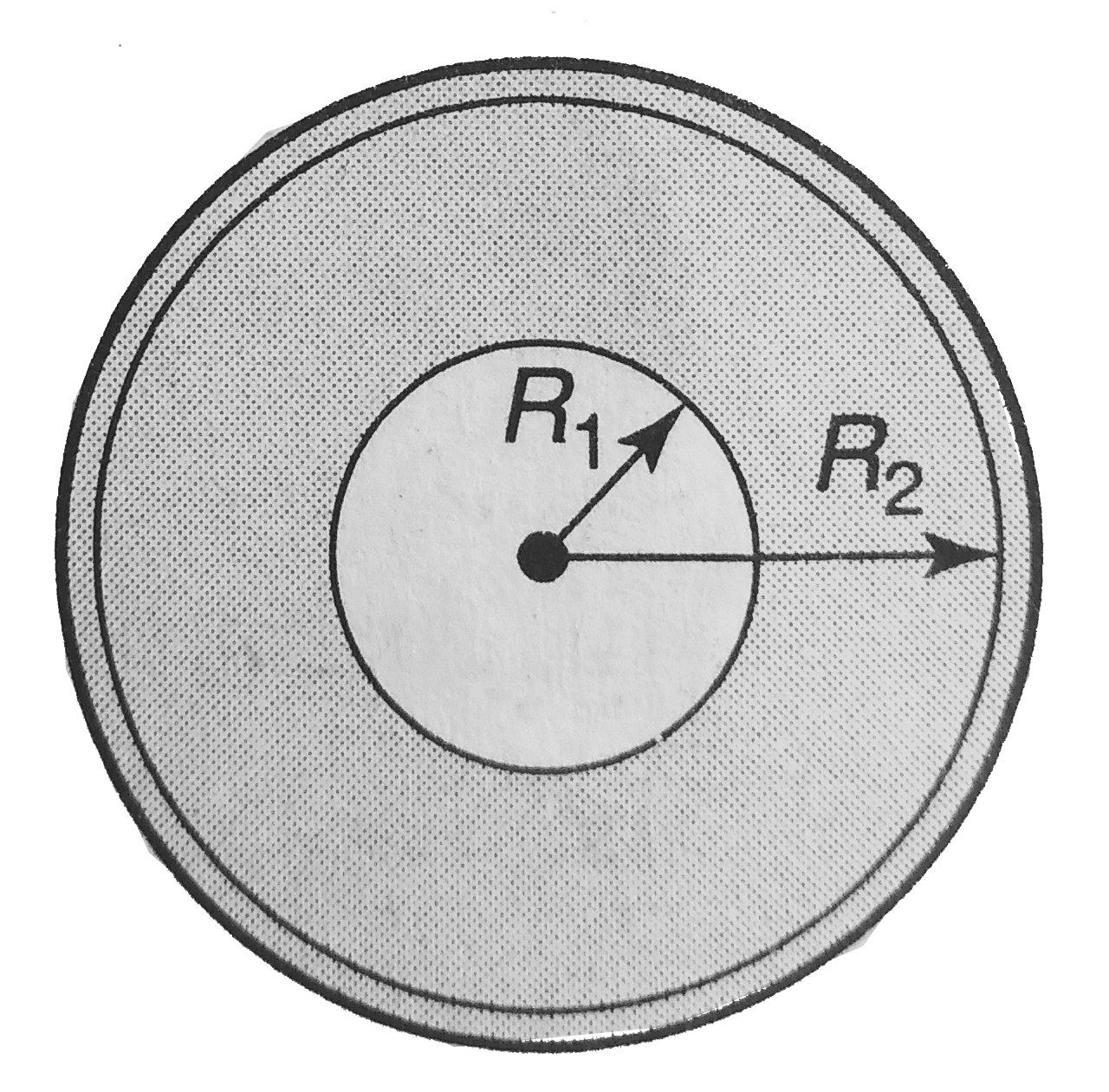
View SolutionA sphare of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
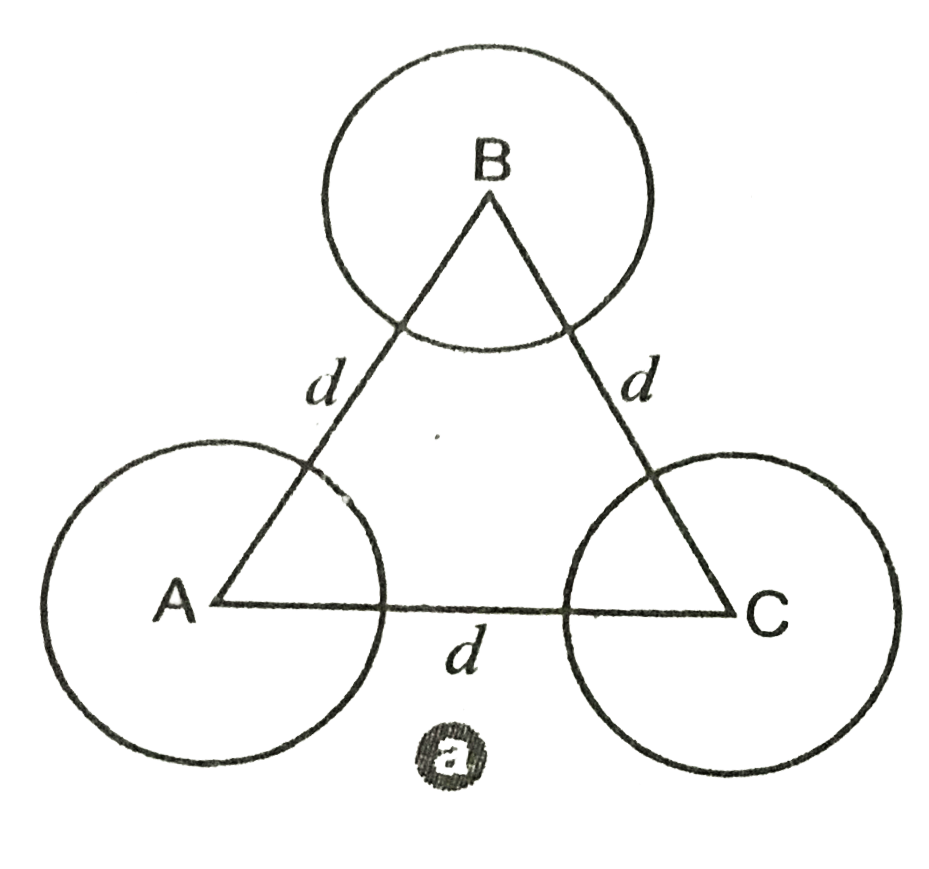
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View Solution
