Match the Column I with Column II
For a satellite in circular orbit
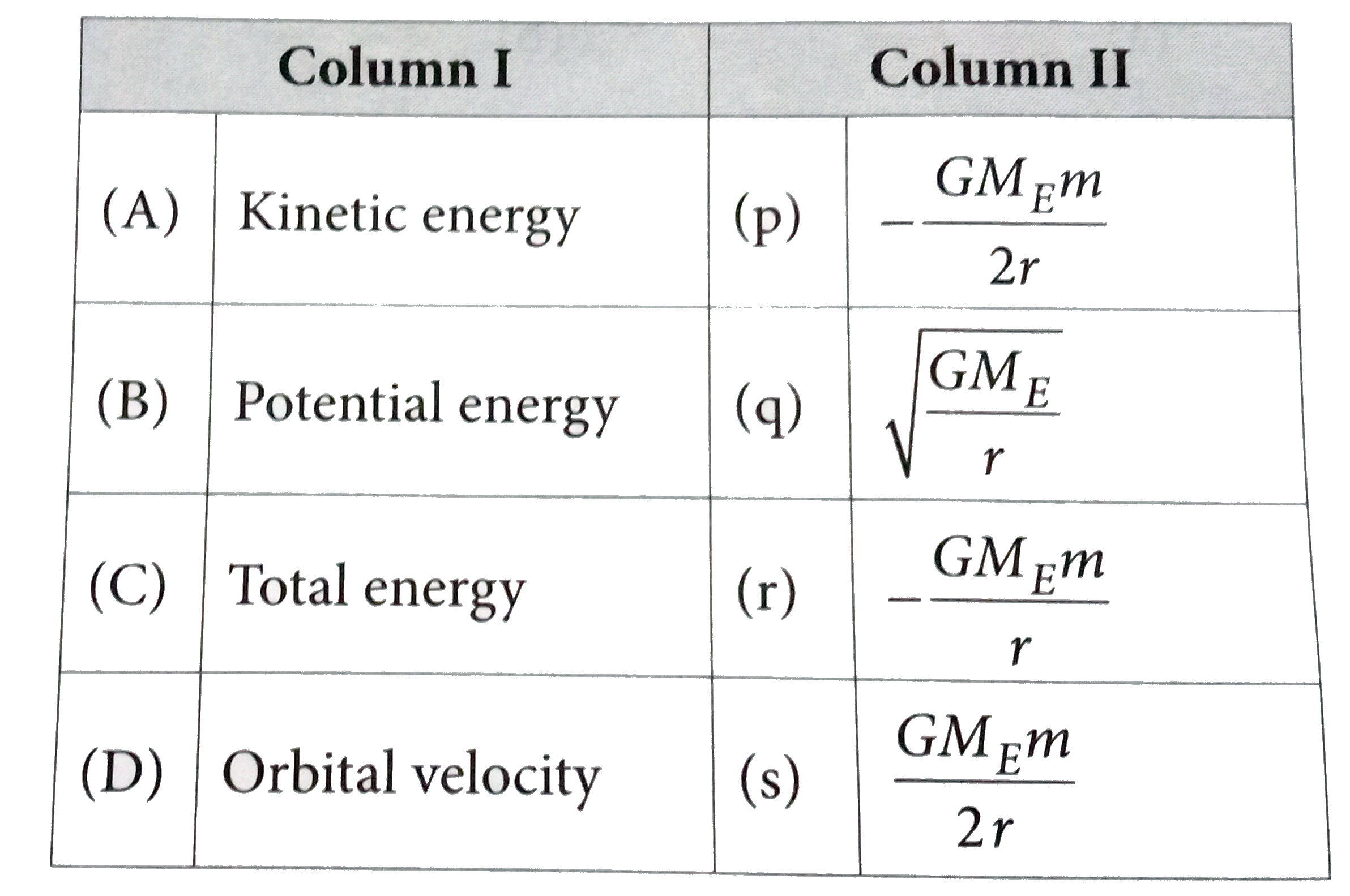
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )
A-r, B-s,C-q,D-p
A-q,B-p,C-r,D-s
A-p,B-q,C-s,D-r
A-s,B-r,C-p,D-q
The correct Answer is:D
(d) Kinetic energy =GMEm2r,A−s
Potential energy =−GMEmr,B−r
Total energy =−GMEm2r,C−p
Orbital velocity =√GMEr,D−q
Topper's Solved these Questions
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Geostationary and Polar satellites
Explore 7 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Weightlessness
Explore 2 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Earth Satellite
Explore 4 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Energy of a satellite in circular orbit is E0. The energy required to move the satellite to a circular orbit of 3 times the radius of the initial orbit is
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View Solution
Knowledge Check
The period of a satellite in a circular orbit of radius R is T. What is the period of another satellite in a circular orbit of radius 4 R ?
A4 TBT/8CT/4D8 TThe orbit of geostationary satellite is circular, the time period of satellite depeds on (i) mass of the satellite, (ii) mass of earth, (iii) radius of the orbit and (iv) height of the satellite from the surface of the earth
A(i) onlyB(i) and (ii)C(i),(ii) and (iii)D(ii),(iii) and (iv)
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View SolutionAn artifical satellite of mass m travels at a constant speed in a circular orbit of radius R around Earth (mass M). What is the speed of the satellite ?
View SolutionAn ariticial satellite (mass =M) of earth revolves in a circular orbit whose radius is 4 times the radius of the earth. Assume that in the spherical region between the radius 4Re and 2Re there is cosmic dust. If mass of the satellite is increasing at the rate of u per sec. Find the time in which satellite will come to orbit of radius 2Re.
View SolutionIt is known that the time of revolution T of a satellite around the earth depends on the universal gravitational constant G, the mass of the earth M, and the radius of the circular orbit R. Obtain an expression for T using dimensional analysis.
View SolutionA satellite of mass m0 is revolving around the earth in circular orbit at a height of 3R from surface of the earth the areal velocity of satellite is (where R is radius of earth and M0 is the mass of earth)
View Solution

