A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
0
10√3 N
30√3N
40√3N
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Understand the Problem
A 1 kg particle strikes a wall at a velocity of 1 m/s at an angle of 60 degrees and reflects off at the same angle. The contact time with the wall is 0.1 seconds. We need to find the force exerted on the particle during the collision.
Step 2: Resolve the Initial Velocity
The initial velocity →u can be resolved into two components:
- The component parallel to the wall (x-direction):
ux=ucos(60∘)=1⋅cos(60∘)=1⋅12=0.5m/s
- The component perpendicular to the wall (y-direction):
uy=usin(60∘)=1⋅sin(60∘)=1⋅√32=√32m/s
Step 3: Determine the Final Velocity Components
After the collision, the particle reflects off the wall with the same speed and angle:
- The x-component of the final velocity vx remains the same in magnitude but changes direction:
vx=−ux=−0.5m/s
- The y-component of the final velocity vy remains the same:
vy=uy=√32m/s
Step 4: Calculate the Change in Momentum
The momentum before and after the collision can be calculated as follows:
- Initial momentum →pi:
→pi=m→u=1⋅(0.5^i+√32^j)=0.5^i+√32^j
- Final momentum →pf:
→pf=m→v=1⋅(−0.5^i+√32^j)=−0.5^i+√32^j
- Change in momentum Δ→p:
Δ→p=→pf−→pi=(−0.5^i+√32^j)−(0.5^i+√32^j)
=−0.5^i−0.5^i+√32^j−√32^j=−1^i+0^j
=−1^ikg m/s
Step 5: Calculate the Force
Using the formula for force:
F=Δ→pΔt
Substituting the values:
F=−1^i0.1=−10^iN
The magnitude of the force is 10N in the negative x-direction.
Final Answer
The force exerted on the particle is 10N in the direction opposite to the initial x-component of the velocity.
---
A 1 kg particle strikes a wall at a velocity of 1 m/s at an angle of 60 degrees and reflects off at the same angle. The contact time with the wall is 0.1 seconds. We need to find the force exerted on the particle during the collision.
The initial velocity →u can be resolved into two components:
- The component parallel to the wall (x-direction):
ux=ucos(60∘)=1⋅cos(60∘)=1⋅12=0.5m/s
- The component perpendicular to the wall (y-direction):
uy=usin(60∘)=1⋅sin(60∘)=1⋅√32=√32m/s
After the collision, the particle reflects off the wall with the same speed and angle:
- The x-component of the final velocity vx remains the same in magnitude but changes direction:
vx=−ux=−0.5m/s
- The y-component of the final velocity vy remains the same:
vy=uy=√32m/s
The momentum before and after the collision can be calculated as follows:
- Initial momentum →pi:
→pi=m→u=1⋅(0.5^i+√32^j)=0.5^i+√32^j
- Final momentum →pf:
→pf=m→v=1⋅(−0.5^i+√32^j)=−0.5^i+√32^j
- Change in momentum Δ→p:
Δ→p=→pf−→pi=(−0.5^i+√32^j)−(0.5^i+√32^j)
=−0.5^i−0.5^i+√32^j−√32^j=−1^i+0^j
=−1^ikg m/s
Using the formula for force:
F=Δ→pΔt
Substituting the values:
F=−1^i0.1=−10^iN
The magnitude of the force is 10N in the negative x-direction.
The force exerted on the particle is 10N in the direction opposite to the initial x-component of the velocity.
Topper's Solved these Questions
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)
Explore 6 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (EQUILIBRIUM OF CONCURRENT FORCES)
Explore 7 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:AIPMT /NEET (MCQ)
Explore 24 Videos
- KINEMATICS Book:MTG GUIDEChapter:KINEMATICS Exercise:AIPMT/ NEET MCQs
Explore 31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Book:MTG GUIDEChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Exercise:AIPMT / NEET (MCQs)
Explore 37 Videos
Similar Questions
A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
View Solution
Knowledge Check
A 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
A96 NB48 NC24 ND40 NA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96NA 3 kg ball strikes a heavy rigid wall with a speed of 10ms−1 at an angle of 60∘ with the wall. It gets reflected with the same speed at 60∘ with the wall. If the ball is in contact with the wall for 0.2s, the average force exerted on the ball by the wall is
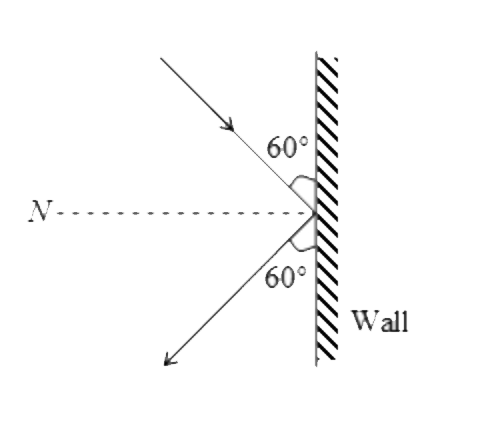 A300NBzeroC150√3ND150 N
A300NBzeroC150√3ND150 N
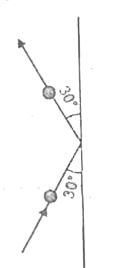
A 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA ball of mass 3 kg collides with a wall with velocity 10 m/sec at an angle of 30° and after collision reflects at the same angle with the same speed. The change in momentum of ball in MKS unit is-
View SolutionA 100g iron ball having velocity 10m/s collies with a wall at an angle 30∘ and rebounds with the same angle. If the period of contact between the ball and wall is 0.1 second, then the force experinced by the wall is
View Solution

