A 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
Zero
40√3N
10√3N
5√3N
To find the force exerted on the wall by the particle, we need to calculate the change in momentum of the particle during the collision and then use the impulse-momentum theorem. Here’s how to do it step by step:
Step 1: Determine the initial and final velocities of the particle.
The particle strikes the wall at a velocity of 1m/s at an angle of 60∘ with respect to the wall. We need to resolve this velocity into components:
- Initial velocity components:
- vix=vicos(60∘)=1⋅cos(60∘)=1⋅0.5=0.5m/s (towards the wall)
- viy=visin(60∘)=1⋅sin(60∘)=1⋅√32≈0.866m/s (upward)
- Final velocity components:
- After reflection, the x-component of the velocity will change direction (it will be negative), while the y-component remains the same:
- vfx=−vix=−0.5m/s
- vfy=viy=0.866m/s
Step 2: Calculate the change in momentum.
Momentum is given by p=mv. We will calculate the change in momentum in the x-direction (since the wall only affects the x-component):
- Initial momentum in the x-direction:
pix=m⋅vix=1⋅0.5=0.5kg m/s
- Final momentum in the x-direction:
pfx=m⋅vfx=1⋅(−0.5)=−0.5kg m/s
- Change in momentum:
Δpx=pfx−pix=−0.5−0.5=−1.0kg m/s
Step 3: Calculate the average force exerted on the wall.
Using the impulse-momentum theorem, the average force F can be calculated using the formula:
F=ΔpΔt
where Δt is the time duration of contact with the wall.
- Given that Δt=0.1s:
F=−1.0kg m/s0.1s=−10N
The negative sign indicates that the force is exerted in the opposite direction of the initial momentum (which is expected as the particle reflects off the wall).
Final Answer:
The average force exerted on the wall by the particle is 10N.
---
- vix=vicos(60∘)=1⋅cos(60∘)=1⋅0.5=0.5m/s (towards the wall)
- viy=visin(60∘)=1⋅sin(60∘)=1⋅√32≈0.866m/s (upward)
- After reflection, the x-component of the velocity will change direction (it will be negative), while the y-component remains the same:
- vfx=−vix=−0.5m/s
- vfy=viy=0.866m/s
pix=m⋅vix=1⋅0.5=0.5kg m/s
pfx=m⋅vfx=1⋅(−0.5)=−0.5kg m/s
Δpx=pfx−pix=−0.5−0.5=−1.0kg m/s
F=ΔpΔt
where Δt is the time duration of contact with the wall.
F=−1.0kg m/s0.1s=−10N
The average force exerted on the wall by the particle is 10N.
Topper's Solved these Questions
Similar Questions
A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
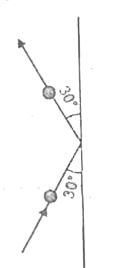
View Solution
Knowledge Check
A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
A0B10√3 NC30√3ND40√3NA 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
A96 NB48 NC24 ND40 NA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96N
A 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA 3 kg ball strikes a heavy rigid wall with a speed of 10ms−1 at an angle of 60∘ with the wall. It gets reflected with the same speed at 60∘ with the wall. If the ball is in contact with the wall for 0.2s, the average force exerted on the ball by the wall is
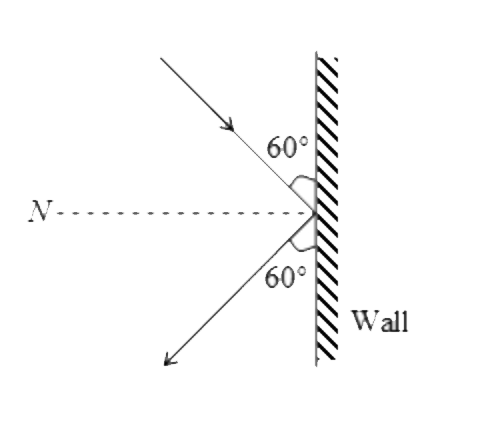
View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA 100g iron ball having velocity 10m/s collies with a wall at an angle 30∘ and rebounds with the same angle. If the period of contact between the ball and wall is 0.1 second, then the force experinced by the wall is
View Solution

