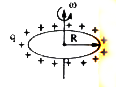
A thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.Solution in Telugu
The equivalent current in the ring is
i=qT=q2πω=qω2π
Magnetic moment
M=ia=qω2π×πR2=qωR22
Angular momentum L=Iω(mR2)ω∴ML=q2m
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IA
Explore 142 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 4 Videos
Similar Questions
Statement (A) : Moving charges produce not only an electric field but also magnetic field in space
Statement (B) : The force is exerted by a magnetic field on moving charges or on a current carrying conductor only but not on stationary charges
View Solution(A) : Magnetic field interacts with a moving charge and not with a stationary charge.
(R) : Magnetic field will be produced by a moving charge but not by a stationary charge.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionIn a sample of rock, the ratio of number of 206Pb to 238U nuclei is found to be 0.5. The age of the rock is (18/n)×109ln(32)ln2 year (Assume that all the Pb nuclides in he rock was produced due to the decay of Uranium nuclides and T1/2(238U)=4.5×109 year). Find n.
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity omega . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA non - conducting charged ring of charge q , mass m and radius r is rotated with constant angular speed omega . Find the ratio of its magnetic moment with angular momentum is
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity omega .Find (ii) Magnetic field produced at the centre of ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA non-conducting charged ring of charge q. mass m and radius r is rotated with constant angular speed omega . Find the ratio of its magnetic moment with angular momentum is ............. .
View SolutionA non-conducting charged ring of charge q. mass m and radius r is rotated with constant angular speed ω. Find the ratio of its magnetic moment with angular momentum is ............. .
View SolutionA non-conducting charged ring of charge q. mass m and radius r is rotated with constant angular speed ω. Find the ratio of its magnetic moment with angular momentum is ............. .
View SolutionCharge Q is uniformly distributed over a nonconducting ring of radius R and mass m. It is made to rotate about an axis passing through its centre and perpendicular to its plone with an angular velocity of rotation omega . Find its magnetic dipole moment and its ratio with angular momentum.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View Solution

