A ballon filled with helium rises against gravity increasing its potential energy . The speed of thee ballon also increases as it rises . How do you reconcile this with the law of conservation of mechanical energy ? You can neglect viscous drag of air and assume that density of air is constant .Solution in Gujrati
m = Mass of ballon
V = Volume of ballon
ρHe = Density of helium
ρair = Denity of air
Volume V of ballon displaces volume V of air .
So , V(ρair−ρHe)g=ma=mdvdt …(i)
Integrating with respect to t ,
⇒V(ρair−ρHe)gt=mv ...(ii)
12mv2=12m(V2m2)(ρair−ρHe)2g2t2
=12mV2(ρair−ρHe)2g2t2
If the ballon rises to a height h ,
from s = ut + 12at2
∴h=12at2
=12V(ρair−ρHe)mgt2(∴u=0)....(iii)
From (iii) and (ii)
12mv2=[V(ρa−ρHe)gt2][12mV(ρair−ρHe)gt2]
=V(ρa−ρHe)gh
Therefore ,
12mv2+VρHe=gh=Vpairhg
KEballon+PEballon = Change in PE of air .
So, as the ballon goes up , an equal volume of air comes down , increase in PE and kE of the ballon is equal to decrease inPE of air .
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - E Multiple Choice Questions (MCQs)
Explore 64 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - F Questions From Module (Sample questions for preparation of competitive exams)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - D NCERT Exemplar Solutions (Short Answer Type Questions)
Explore 10 Videos
- WAVESBook:KUMAR PRAKASHANChapter:WAVESExercise:SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
Explore 23 Videos
Similar Questions
The potential energy of 1 kg particle , free to move allong is given by U(x)=(x33−x22)I. if its mechanical energy is 2J . Its maximum speed is …… ms−1
View SolutionA Sphere makes an inslastic collision with another sphere of same mass , then both the spheres are moving .The angle between their direction of motion will be ……..
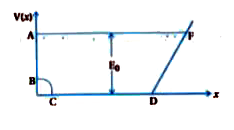
View SolutionA graph of potential energy V(x) verses x is shown in figure .A particle of energy E0 is executing motion in it . Draw graph of velocity and kinetic energy verses x for one complete cycle AFA.
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionWhen an air bubble rises in water, what happens to its potential energy /
View SolutionA baloon filled with helium rises against gravity increasing its potential energy. The speed of the baloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy ? You can neglect viscous drag of air and assume that density of air is constant.
View SolutionA helium ballon occupies 8.0 L at 20^(@)C and 1.0- atm pressure. The ballon rises to an altitude where the air pressure is 0.65 atm and the temperature is -10^(@)C . What is its volume when it reaches equilibrium at the new altitude? Note: Neglect tension forces in te material of the balloon.
View SolutionA rope ladder of length L is attached to ballon of mass m. As the man of mass m clims the ladder in to the lballon basket the ballon comes donws by a vertical distance s. Then increase in potential energy of man divided by increase inn potential energy of ballon is
View SolutionRam took an empty ballon of mass 5 g and filled it with air. He then measured the mass of ballon filled with air tube to be 5.05 g. He considered the density of the air filled inside th ballon as 1.5 kg m−3 and found the volume of air present inside the ballon. Find his answer.
View SolutionDefine mechanical energy and law of conservation of mechanical energy. Prove conversion of gravitational potential energy in to kinetic energy by the help of law of conservation of mechanical energy. Also draw graph between energy and height.
View Solutionयांत्रिक ऊर्जा संरक्षण से आप क्या समझते है ?
View SolutionThe hot air ballon rises because it is
View Solutionहीलियम से भरा गुब्बारा गुरुत्व के विरुद्ध ऊपर उठता है। जिससे इसकी स्थितिज ऊर्जा में वृद्धि हो जाती है। जैसे-जैसे गुब्बारा ऊपर जाता है इसकी चाल भी बढ़ जाती है। इस प्रेक्षण का तालमेल आप यांत्रिक ऊर्जा संरक्षण के नियम से कैसे बैठाएंगे? आप वायु के श्यान कर्षण की उपेक्षा कर सकते हैं और यह मान सकते हैं कि इसका घनत्व नहीं बदलता।
View SolutionA ballon filled with hydrogen rises upward gaining both kinetic and potential energy.Does it imply violation of conservation of energy?
View SolutionWhen an air bubble rise in water, what happens to its potential energy?
View Solution

