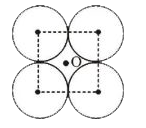
Four solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of $I_{0}$ & $I_{A}$ , where $I_{0}$ is the moment of inertia of the system about an axis through the centre of the square and $I_{A}$ is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)

$\frac{6}{11}$

$\frac{4}{11}$

$\frac{5}{11}$

$\frac{7}{11}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Moment of inertia of a rigid body about an axis passing through its centre of mass is $I_{0}$ and moment of inertia of the same body about another axis parallel to the first axis is I. Then
AI is always equal to $I_{0}$
BI is always smaller than $I_{0}$
CI is always greater than $I_{0}$
Dany of the above three
Four identical thin rods each of mass $M$ and length $l$ , from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
A $\frac{1}{3} M l^{2}$
B $\frac{4}{3} M l^{2}$
C $\frac{2}{3} M l^{2}$
D $\frac{13}{3} M l^{2}$
Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then the moment of inertia of the system about an axis along one of the sides of the square is
A $\frac{4}{5} M a^{2} + 2 M b^{2}$
B $\frac{8}{5} M a^{2} + 2 M b^{2}$
C $\frac{8}{5} M a^{2} + M b^{2}$
D $\frac{4}{5} M a^{2} + 4 M b^{2}$