Question

Obtain the position of centre of mass of a thin rod of uniform density.

Explanation

Homogeneous body means a body with uniformly distributed mass.
Let us consider a thin rod, whose width and breadth (in case of cross-section of the rod is rectangular) or radius (In case of the cross section of the rod is cylindrical) is much smaller than its length.
Taking the origin to be at the geometric centre of the rod and X-axis to be along the length of the rod, for every element dm of the rod at `+x` there is an element of the same mass dm located at `-x`.

The net contribution of every such pair to the integral and hence the integral. `intxdm` itself in zero.
`therefore` Centre of mass of rod,
`X=(1)/(M)intxdm`
but `dm=lambdadx`
where `lambda` = mass per unit length = `(M)/(L)`
`=(M)/(L)dx` where L = length of rod,
`therefore X=(1)/(M)intx(M)/(L)dx`
`=(1)/(L)underset(0)overset(1)intxdx`
`=(1)/(L)[(x^(2))/(2)]_(0)^(L)`
`=(1)/(L)[(L^(2))/(2)]`
`=(1)/(2)`.
Hence, centre of mass of thin rod of uniform density lies at midpoint of the length of rod means at its geometric centre.
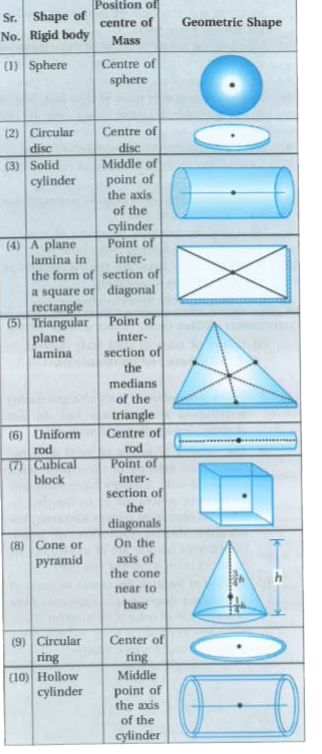
Centre of mass of homogeneous ring, disc and spheres can be found in this way and above all bodies their centre of mass coincide with their geometric centre.
Position of centre of mass of bodies of regular shape :