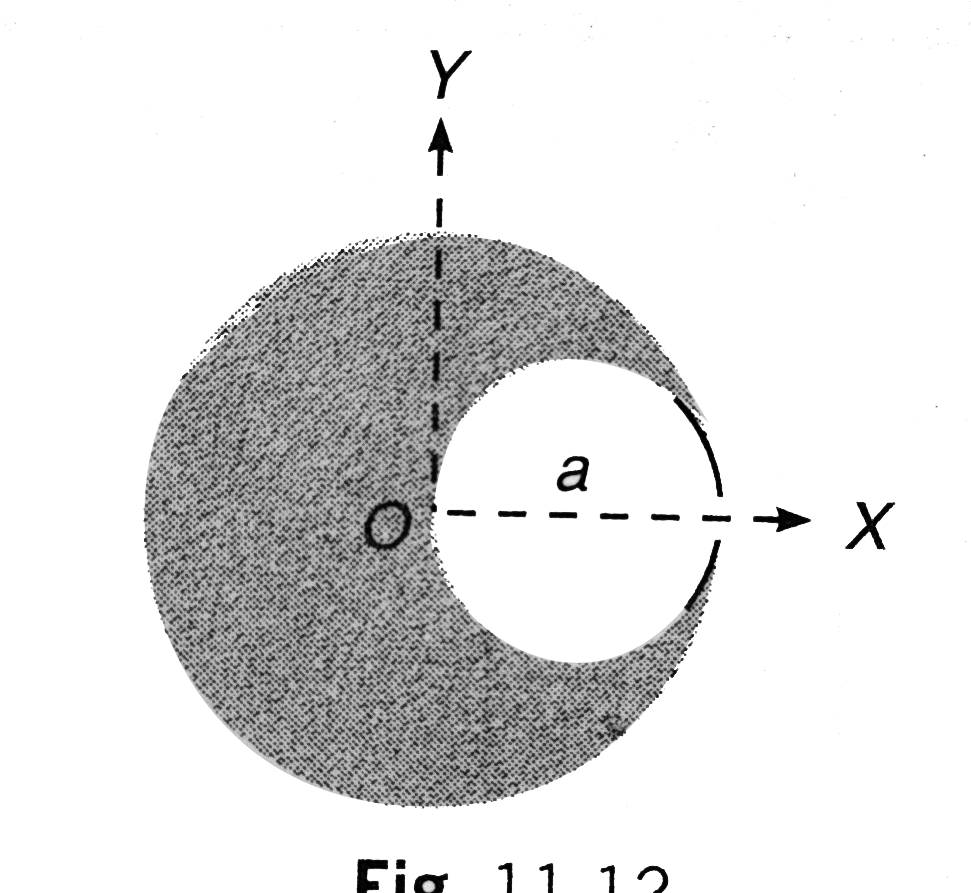
The position of the centre of mass of a cube of uniform mass density will be at
the centre of one face
the centre of the interaction of diagonals of one face.
the geometric centre of the cube
the edge of a cube
The correct Answer is:c
To determine the position of the center of mass of a cube with uniform mass density, we can follow these steps:
Step 1: Understand the Concept of Center of Mass
The center of mass of an object is the point at which the mass of the object can be considered to be concentrated. For symmetrical objects with uniform mass density, the center of mass is located at the geometric center.
Step 2: Identify the Geometry of the Cube
A cube has six faces, twelve edges, and eight vertices. The geometric center of a cube can be found by locating the midpoint of the cube's dimensions.
Step 3: Calculate the Geometric Center
For a cube with side length 'a':
- The coordinates of the vertices can be taken as (0,0,0), (a,0,0), (0,a,0), (0,0,a), (a,a,0), (a,0,a), (0,a,a), and (a,a,a).
- The geometric center (or centroid) can be calculated as the average of the coordinates of the vertices.
Step 4: Find the Coordinates of the Center of Mass
The coordinates of the center of mass (CM) can be calculated as follows:
- CM_x = (0 + a + 0 + 0 + a + a + 0 + a) / 8 = a/2
- CM_y = (0 + 0 + a + 0 + a + 0 + a + a) / 8 = a/2
- CM_z = (0 + 0 + 0 + a + 0 + a + a + a) / 8 = a/2
Thus, the center of mass of the cube is located at the point (a/2, a/2, a/2), which is the geometric center of the cube.
Step 5: Conclusion
Since the center of mass of a cube with uniform mass density is located at its geometric center, the correct answer is:
The geometric center of the cube.
The center of mass of an object is the point at which the mass of the object can be considered to be concentrated. For symmetrical objects with uniform mass density, the center of mass is located at the geometric center.
A cube has six faces, twelve edges, and eight vertices. The geometric center of a cube can be found by locating the midpoint of the cube's dimensions.
For a cube with side length 'a':
- The coordinates of the vertices can be taken as (0,0,0), (a,0,0), (0,a,0), (0,0,a), (a,a,0), (a,0,a), (0,a,a), and (a,a,a).
- The geometric center (or centroid) can be calculated as the average of the coordinates of the vertices.
The coordinates of the center of mass (CM) can be calculated as follows:
- CM_x = (0 + a + 0 + 0 + a + a + 0 + a) / 8 = a/2
- CM_y = (0 + 0 + a + 0 + a + 0 + a + a) / 8 = a/2
- CM_z = (0 + 0 + 0 + a + 0 + a + a + a) / 8 = a/2
Since the center of mass of a cube with uniform mass density is located at its geometric center, the correct answer is:
The geometric center of the cube.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:MOTION OF CENTRE OF MASS
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:TORQUE AND ANGULAR MOMENTUM
Explore 11 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- PRACTICE PAPERSBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPERSExercise:All Questions
Explore 150 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Knowledge Check
The x, y coordinates of the centre of mass of a uniform L-shaped lamina of mass 3 kg is
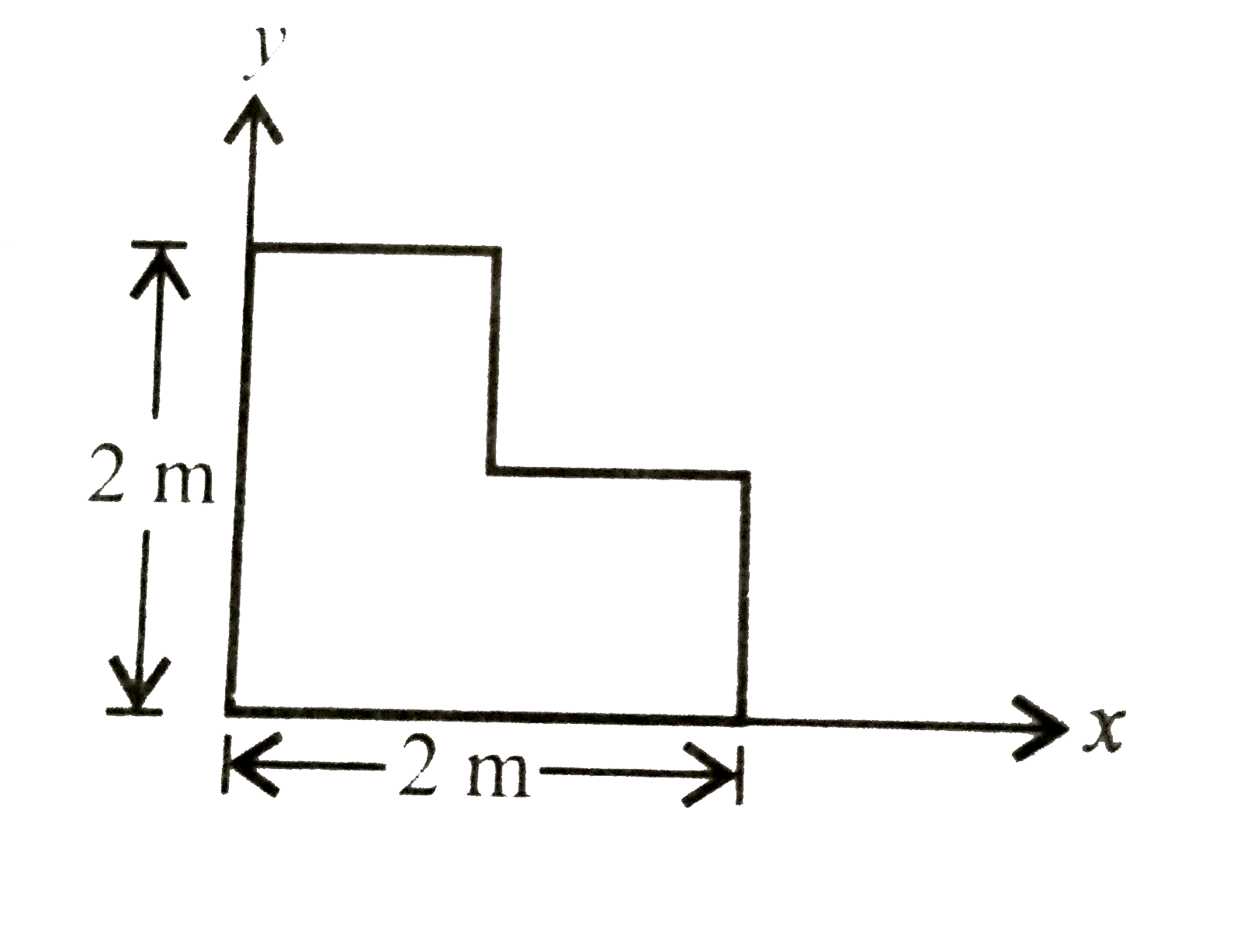 A(5/6 m, 5/6 m)B(1 m, 1 m)C(6/5 m, 6/5 m)D(2 m, 2m)
A(5/6 m, 5/6 m)B(1 m, 1 m)C(6/5 m, 6/5 m)D(2 m, 2m)
The position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionThe distance of the centre of mass of T-shaped uniform plate from O is :
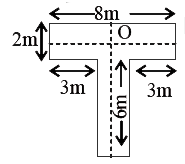
View SolutionIf the linear mass density of a rod of length 3 m (lying fromy=0 toy=3m) varies as λ=(2+y)kg/m,then position of the centre of mass of the rod from y=0 is nearly at
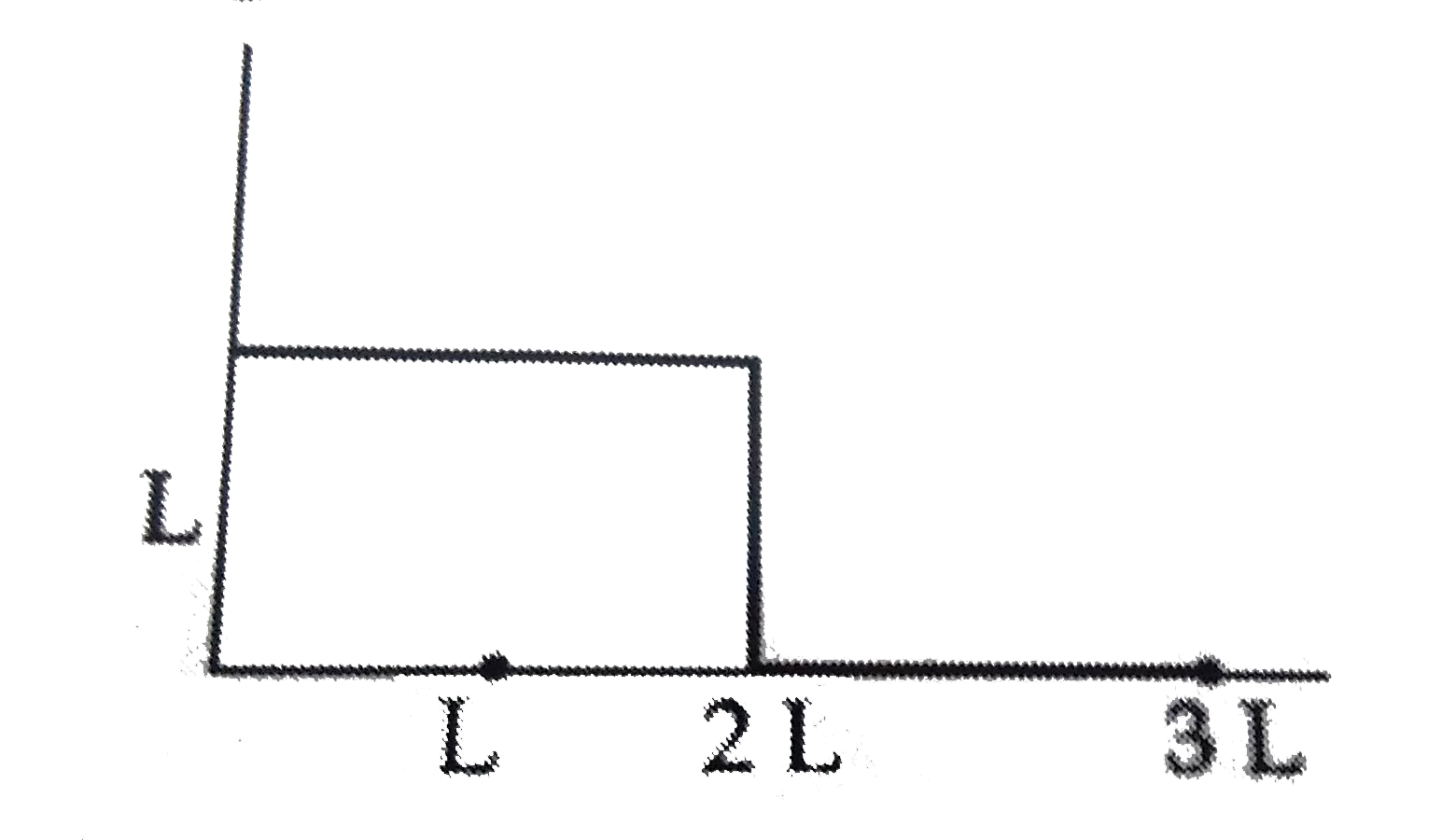
View Solutionthe position vector of the centre of mass lt
→
r cm of an asymmetric uniform bar of negligible area of cross - section as shown in figure is :
View SolutionWhat is the location of the centre of mass of a uniform triangular lamina ?
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionFind the position of centre of mass of the section shown in figure

View Solution