A transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is Solution in Telugu
9:7
9:49
3:7
7:3
The correct Answer is:B
Step by step video, text & image solution for A transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000 A^(@), the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED )staright Objective Type Questions30videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) More than one correct answer Type Questions4videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise (Practice Sheet (Advanced))6videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)81videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
White light is passed through a double slit aand interference pattern is observed on a screen 2.5 away. The separation between the slits is 0.5 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringe. Calculate the wavelengths of the violet and the red light.
05:17View SolutionIn the Young.s double slit experiment set up , source S of wavelength 500 nm illuminates two slitS1andS2 which set as two coherent sources . The source S oscillates about its own position according to the equation y = 0.5 sinπt where y is in mm and t in seconds . the minimum value of time t for which the intensity at point p on the screen exactly infront of the upper slit becomes minimum is which the intensity at point P on teh screen exactly infornt of the upper slit becomes minimum is
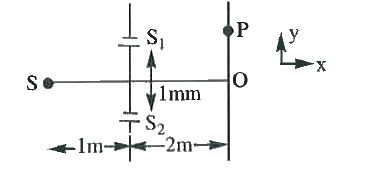 01:53View Solution
01:53View SolutionA slit 5 cm wide is irradiated normally with microwaves of wavelength 1.0 cm. Then the angular instead of central maximum on either side of incident light is nearly
02:44View SolutionA wave is described by the equation
y=(1.0mm)sinπ(x2.0cm−10.01s)
Find the time period and the wavelength.08:34View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s)
02:59View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
02:58View SolutionDetermine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is lambda/(2(mu-1)) , where lambda is the wavelength of the incident light and mu is the index of refraction of the film.
05:13View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
08:18View SolutionA YDSE is performed in a medium of refractive index 4 // 3 , A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S_(2) is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4 // 3 , ignore absorption.) Find the light intensity at point O relative t maximum fringe intensity.
01:50View SolutionIn Young's double slit experiment, a glass plate is placed before a slit which absorbs half the intensity of light. Under this case
04:20View SolutionA double slit experiment is done with monochromatic light of wavelength 6000 Å . Slits are 2 mm apart and fringes are observed on a screen placed 10 cm away from the slits. If a transparent plate of thickness 0.5 mm is placed in front of one of the slit, interference pattern shifts by 5 mm. Then refractive index of transparent plate should be :
01:50View SolutionIn an ideal double slit experiment when a glass plate having refractive index 1.5 and thickness t is placed in the path of interfered light rays of wavelength λ then the intensity remains unchanged at the place where the central maximum was previously formed. Then the minimum thickness of the glass plate is
01:48View SolutionA thin glass plate of thickness is 25003λ (λ is wavelength of light used) and refractive index μ=1.5 is inserted between one of the slits and the screen in Young's double slit experiment. At a point on the screen equidistant from the slits, the ratio of the intensities before and after the introduction of the glass plate is :
02:23View SolutionA transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000 A^(@) , the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
03:53View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
01:30View Solution


