A charge q is uniformly distributed throught the volume of a sphere R and permittvity k = 1. Let U1andU2 be the electrostatic energy within and outside ths sphere. Then U1:U2 is equal to 1/x where .x. is Solution in Telugu
The correct Answer is:5
Step by step video, text & image solution for A charge q is uniformly distributed throught the volume of a sphere R and permittvity k = 1. Let U_(1) and U_(2) be the electrostatic energy within and outside ths sphere. Then U_(1) : U_(2) is equal to 1/x where .x. is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 4 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II STRAIGHT OBJECTIVE TYPE QUESTION)
Explore 8 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
Explore 3 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 6 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 9 Videos
Similar Questions
4 charges are placed each at a distance .a. from origin. The distance .a. from origin. The dipole moment of configuration is :
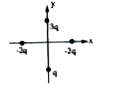
View SolutionA short pˆi is placed at origin in x - y plane. The locus of equipotential surface around the dipole if a constant electric field Eˆi also exists through out the space is (k=14πε0)(Vorigin=0)

View SolutionIf a charge is moving towards the centre of an earthed conducting sphere of radius b with uniform velocity v. Distance of two points A and B from centre of sphere are 3a & 2a. Conducting sphere is earthed with an ammeter and resistance in series (as shown)

Potential of the sphere will be
View SolutionWhat is the radius of the path of an electron (mass 9 × 10-31 kg and charge 1.6×x10–19 C) moving at a speed of 3×x107 m/s in a magnetic field of 6x×10−4 T perpendicular to it? What is its frequency? Calculate its energy in keV. (1eV=1.6×10−19J)
View SolutionFind the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
View SolutionIf u_(1),u_(2),u_(3),... forms a G.P with common ratio k then find the sum of u_(1)u_(2)+u_(2)u_(3)+...u_(n)+u_(n+1) in terms of u_(1) and k
View SolutionIn the previous problem , sphere A is moving with speed u_(1) and sphere B with speed u_(2) in opposite direction. After the collision , sphere A comes to rest , then u_(1)//u_(2) is
View SolutionIn a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U_(0) joules then find out self energy of sphere in term of U_(0) ?
View SolutionLet A=((1,0,0),(2,1,0),(3,2,1)) . If u_(1) and u_(2) are column matrices such that Au_(1)=((1),(0),(0)) and Au_(2)=((0),(1),(0)) , then u_(1)+u_(2) is equal to :
View SolutionFor a certain function ux, given that u0=3,u1=12,u2=81,u3=200,u4=100,u5=8, then Δ5ux is equal to
View SolutionFor the sequence {un} if u1=14 and un+1=un2+un, find the value of 1u50.
View SolutionIf u1,u2,u3,… form a G.P. with common ratio k, find the sum of u1u2+u2u3+….+unun+1 in terms of u1 and k.
View SolutionIf nεN and u1=xn,u2=xn−1,u3=xn−2,...,un=x, then u1'.u2'.u3...un'=
View SolutionLet A=((1,0,0),(2,1,0),(3,2,1)) . If u_(1) and u_(2) are column matrices such that Au_(1)=((1),(0),(0)) and Au_(2)=((0),(1),(0)) then u_(1)+u_(2) is equal to
View SolutionThe answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit. There is one charged metallic sphere of radius R. The charge is uniformly distributed over its surface. Let U_(1) be the energy stored in the region from radius R (surface) up to the radius 2R and U_(2) be the total energy stored outside this sphere. Calculate U_(2)//U_(1) .
View Solution
