In a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U0 joules then find out self energy of sphere in term of U0 ?
To find the self-energy of a uniformly charged solid sphere in terms of the energy stored outside the sphere, denoted as U0, we can follow these steps:
Step 1: Understand the Problem
We have a uniformly charged solid sphere with total charge Q and radius R. The energy stored outside the sphere is given as U0. We need to find the total self-energy of the sphere, which includes both the energy inside and outside the sphere.
Step 2: Energy Stored Outside the Sphere
The energy stored outside the sphere can be expressed as:
U0=Q28πϵ0R
This expression comes from integrating the electric field due to the sphere from infinity to the surface of the sphere.
Step 3: Energy Stored Inside the Sphere
For the energy stored inside the uniformly charged sphere, we need to consider the electric field inside the sphere. The electric field E at a distance x from the center (where x<R) is given by:
E=Q4πϵ0R3x
The energy density u inside the sphere can be calculated using:
u=12ϵ0E2
Substituting the expression for E:
u=12ϵ0(Q4πϵ0R3x)2
Step 4: Calculate Total Energy Inside the Sphere
To find the total energy inside the sphere, we integrate the energy density over the volume of the sphere:
Uinside=∫R0u⋅dV
The volume element dV for a spherical shell of radius x and thickness dx is 4πx2dx. Therefore:
Uinside=∫R012ϵ0(Q4πϵ0R3x)24πx2dx
This simplifies to:
Uinside=Q28πϵ0R3∫R0x4dx
Calculating the integral:
∫R0x4dx=R55
Thus:
Uinside=Q28πϵ0R3⋅R55=Q2R240πϵ0
Step 5: Relate Inside Energy to U0
Now, we can express Uinside in terms of U0:
Uinside=15U0
Step 6: Total Self-Energy of the Sphere
The total self-energy Utotal of the sphere is the sum of the energy inside and outside:
Utotal=Uinside+U0=15U0+U0=65U0
Final Answer
Thus, the self-energy of the uniformly charged sphere in terms of U0 is:
Uself=65U0
We have a uniformly charged solid sphere with total charge Q and radius R. The energy stored outside the sphere is given as U0. We need to find the total self-energy of the sphere, which includes both the energy inside and outside the sphere.
The energy stored outside the sphere can be expressed as:
U0=Q28πϵ0R
This expression comes from integrating the electric field due to the sphere from infinity to the surface of the sphere.
For the energy stored inside the uniformly charged sphere, we need to consider the electric field inside the sphere. The electric field E at a distance x from the center (where x<R) is given by:
E=Q4πϵ0R3x
The energy density u inside the sphere can be calculated using:
u=12ϵ0E2
Substituting the expression for E:
u=12ϵ0(Q4πϵ0R3x)2
To find the total energy inside the sphere, we integrate the energy density over the volume of the sphere:
Uinside=∫R0u⋅dV
The volume element dV for a spherical shell of radius x and thickness dx is 4πx2dx. Therefore:
Uinside=∫R012ϵ0(Q4πϵ0R3x)24πx2dx
This simplifies to:
Uinside=Q28πϵ0R3∫R0x4dx
Calculating the integral:
∫R0x4dx=R55
Thus:
Uinside=Q28πϵ0R3⋅R55=Q2R240πϵ0
Now, we can express Uinside in terms of U0:
Uinside=15U0
The total self-energy Utotal of the sphere is the sum of the energy inside and outside:
Utotal=Uinside+U0=15U0+U0=65U0
Thus, the self-energy of the uniformly charged sphere in terms of U0 is:
Uself=65U0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Figure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.

View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionFigure shows a hemisphere of charge Q and radius R and a sphere of charge 2Q and radius R. The total potential energy of hemisphere is UH and that of the sphere is Us Then.
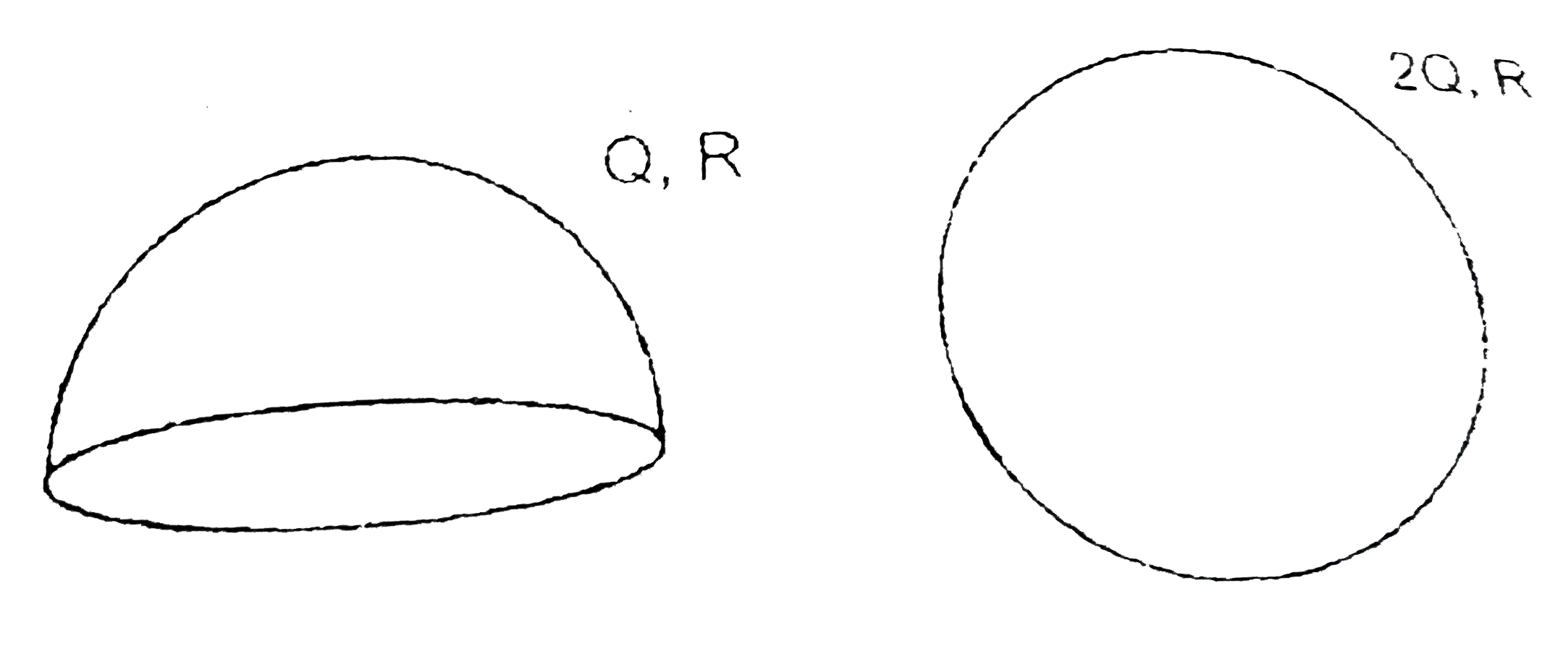
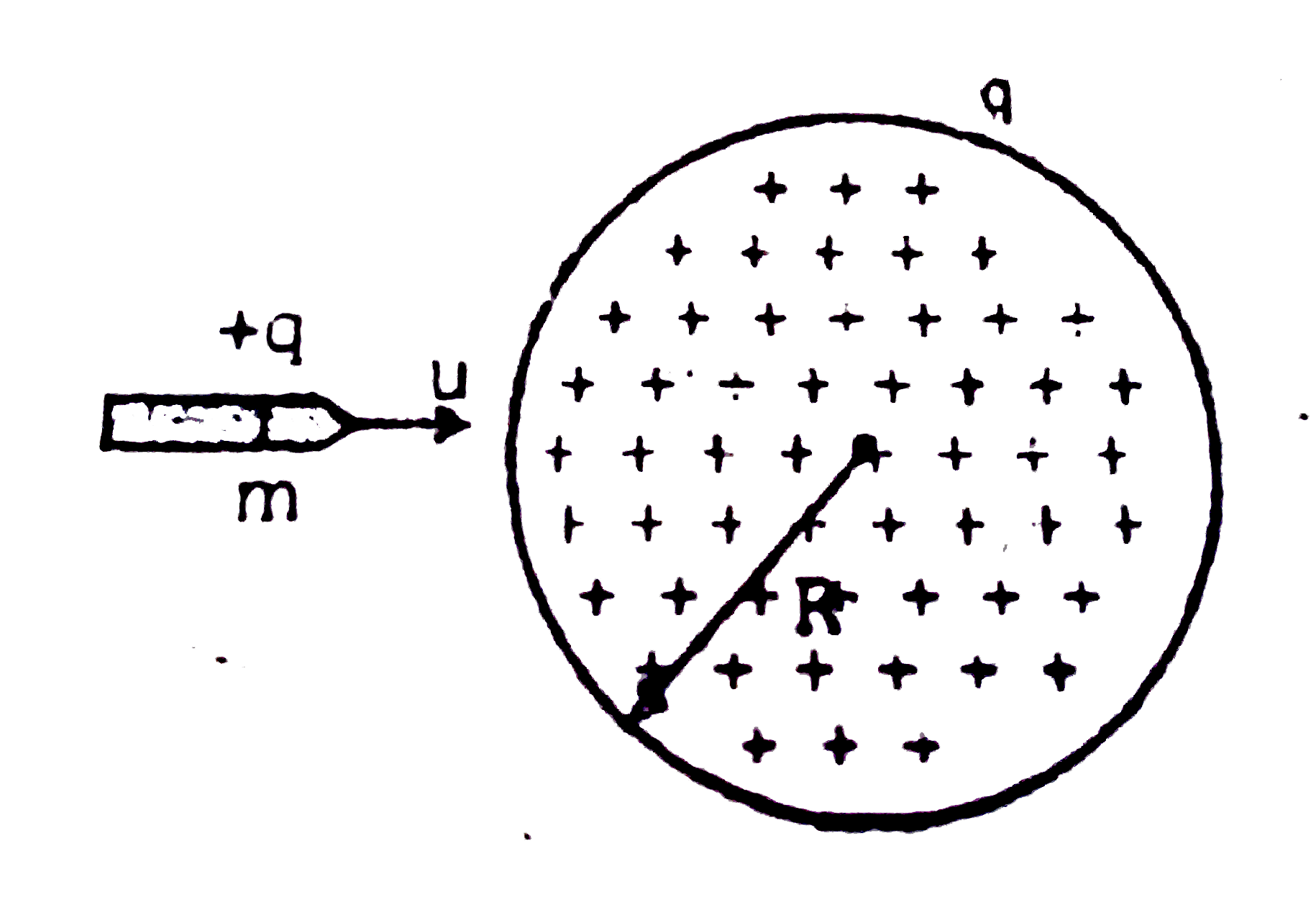
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionFigure shows a uniformly charged thin non-conducting sphere of total charge Q and radius R. If point charge q is situated at point 'A' which is at a distance r<R from centre of the sphere, then find out following :
(i) Force acting on charge q.
(ii) Electric field at centre of sphere.
(iii) Electric field at point B.

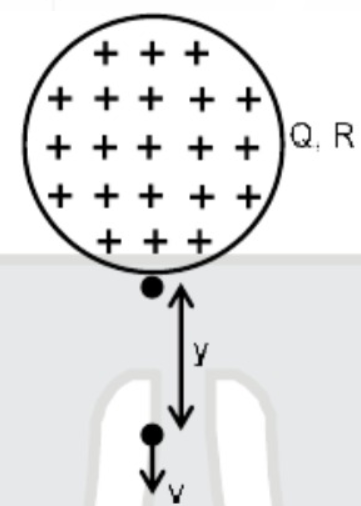
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphere
View SolutionTwo non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.

View Solution
