Two coherent fight sources A and B with separation 2λ are placed on the x-axis symme-trically about the origion. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and with centre at the origion.
For P to have maximum intensity, dcosθ=nλ
2λcosθ=nλ cosθ=n2
where n is integer
For n=0,θ=90∘,270∘
n=±1,θ=60∘,120∘,240∘,300∘
n=±2,θ=0∘,180∘
So, position of maxima are at
θ=0∘,60∘,120∘,180∘,240∘,270∘ and 300∘
i.e., 8 positions will be obtained.
Short cut : In d=nλ then number of maximum on the circle is 4n.
Topper's Solved these Questions
Similar Questions
Two coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
View SolutionAn inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the total number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?

View Solution
Knowledge Check
Two coherent sources A & B emitting light of wavelength lambda are placed at position (-D,0) and (−D,3λ) respectively Here D >>λ The number of minima on y-axis and maxima on x-axis respectively are
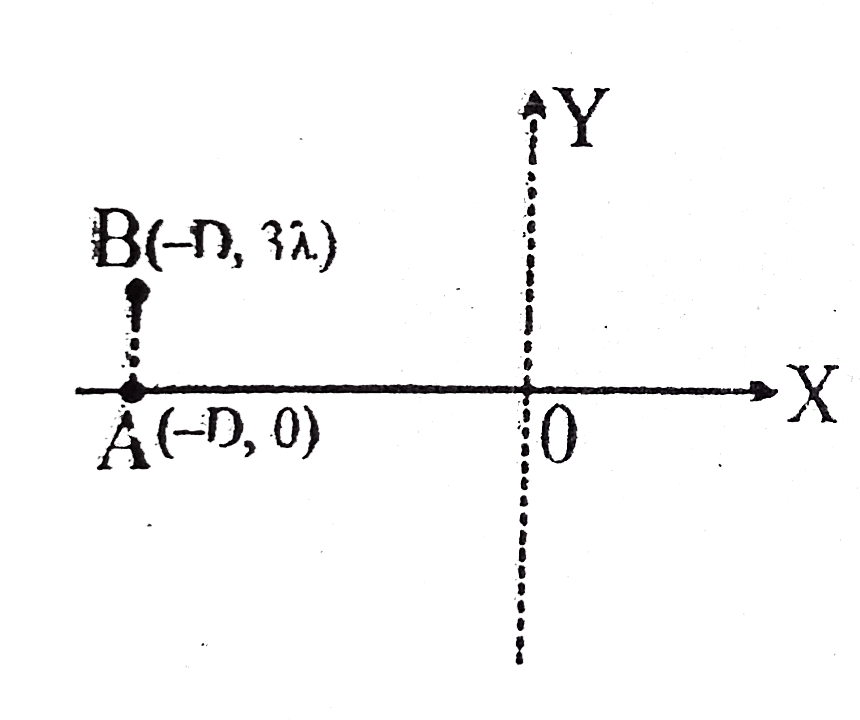 A6,5B5,6C4,3D3,4
A6,5B5,6C4,3D3,4Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
A20B22C24D26Two coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
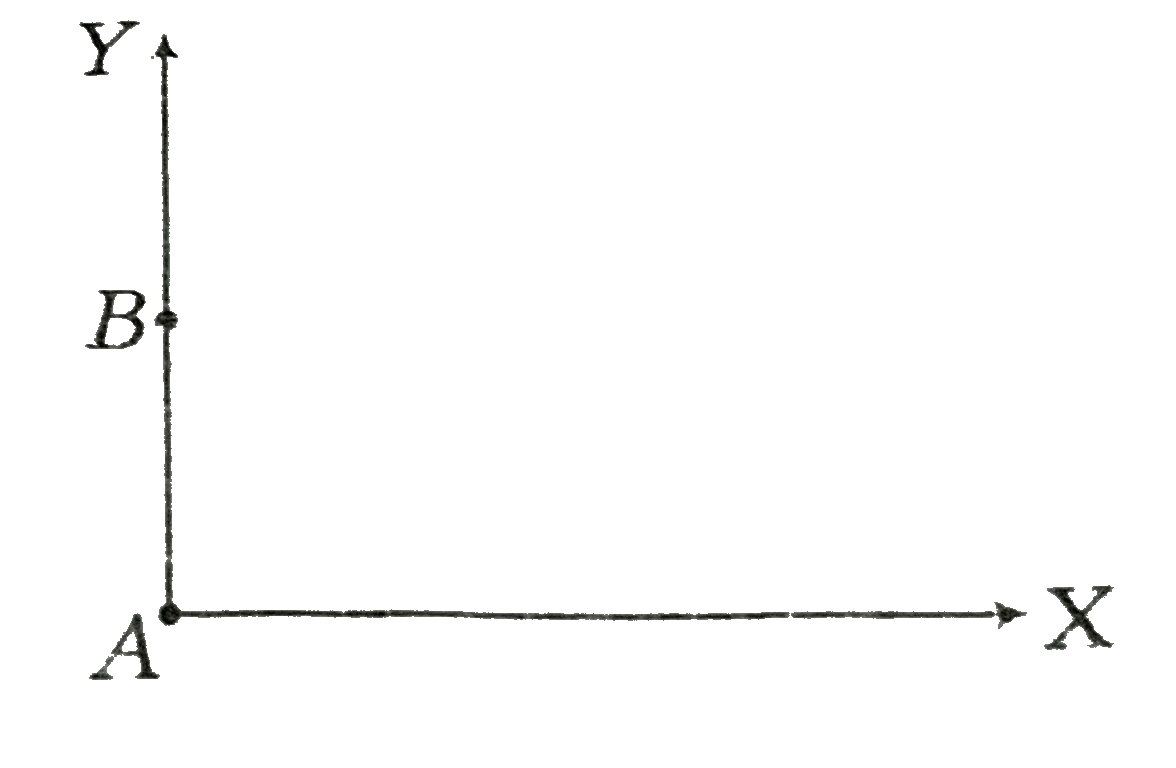 A3λB8λC5λ/4D8.75λ
A3λB8λC5λ/4D8.75λ
Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=5λ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are

View SolutionAn inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the totla number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?

View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=nλ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View Solution

