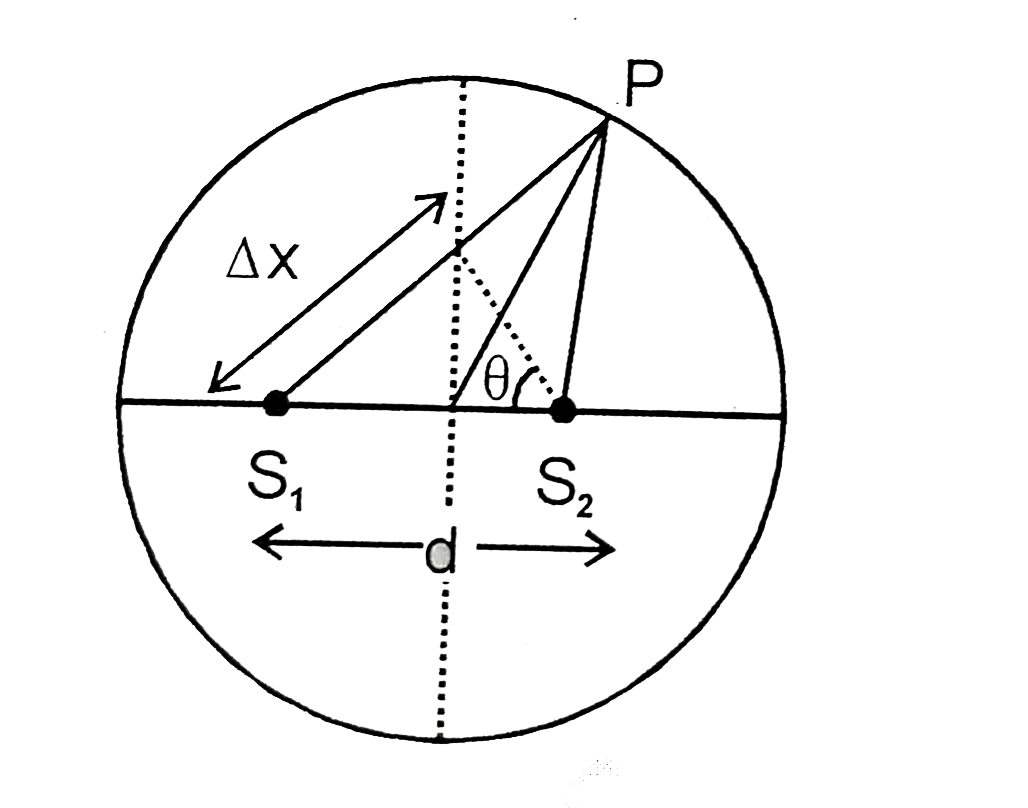
Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=nλ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
2n+1
4n
4n−2
4n+2
The correct Answer is:B
For maxima sinθ=nλd
⇒θ=sin−1(nλd)
So, no. of maxima in first quadrant is dλ. In second quadrant is dλ
So, in total no. of maximum =4dλ but out of these two are counted together so, actual no =4dλ−2
Topper's Solved these Questions
Similar Questions
Two point charge each +3 µC are placed along the diameter of a circle of radius 15 cm. Calculate the ectric potential at the ends of perpendicular diameter
View SolutionTwo coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
View Solution
Knowledge Check
Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
A20B22C24D26Two sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
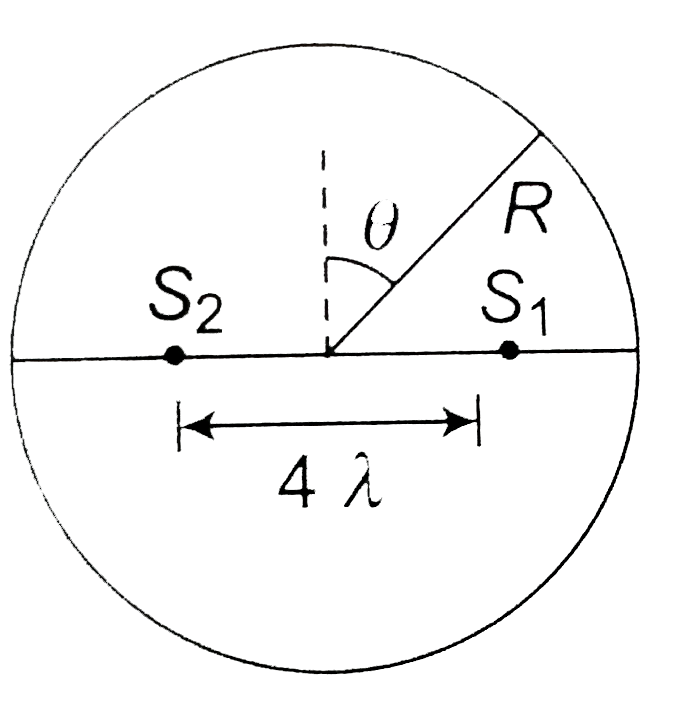A12B16C4D20Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
A(a) Their phase differences remain constantB(b) Their phases are distributed randomlyC(c) Their light intensities remain constantD(d) Their light intensities change randomly
In the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ?
View SolutionIf two coherent source are placed at a distance 3λ from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?
View SolutionFour point charges each +q is placed on the circumference of a circle of diameter 2d in such a way that they form a square. The potential at the centre is
View SolutionA charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. The ratio of electric potentials at the centre in the two situations is
View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View Solution