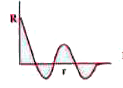
When Schrodinger wave equation in polar coordinates is solved the solution for $Φ$ is of the form $Ψ (r, θ, ϕ) = R (r), Y (θ, ϕ)$ . Here R(r) is radial part of wave function and $Y (θ, ϕ)$ is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then $Ψ^{2} (r, θ, ϕ) = 0 \Rightarrow Ψ (r, θ, ϕ) = 0$
If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number.
represents Solution in Telugu

$6 d_{x y}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

For same n values , distance depends on l value as l value increase distance increases

Updated on:21/07/2023

Class 11 CHEMISTRY STRUCTURE OF ATOM

Similar Questions

यदि $x = r sin θ cos ϕ, y = r sin θ sin ϕ$ तथा $z = r cos θ$ हो, तो:
View Solution
If $x = r cos θ sin ϕ, y = r sin θ sin ϕ$ , and $z = r cos ϕ$ , prove that $x^{2} + y^{2} + z^{2} = r^{2}$ .
View Solution
In Schrodinger wave mechanical model $Ψ^{2}$ $(r, θ, ϕ)$ represents :
View Solution
When Schrodinger wave equation in polar coordinates is solved the solution for Phi is of the form Psi (r, theta , phi)= R(r) , Y(theta , phi) . Here R(r) is radial part of wave function and Y(theta, phi) is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then Psi^2 (r, theta, phi)=0 implies Psi (r, theta, phi)=0 If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number. The d-orbital with two nodal surfaces formed cones
View Solution
When Schrodinger wave equation in polar coordinates is solved the solution for $Φ$ is of the form $Ψ (r, θ, ϕ) = R (r), Y (θ, ϕ)$ . Here R(r) is radial part of wave function and $Y (θ, ϕ)$ is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then $Ψ^{2} (r, θ, ϕ) = 0 \Rightarrow Ψ (r, θ, ϕ) = 0$
If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number.
Number of radial nodes for 4f orbital
View Solution
Psi^2 (r , theta , phi) represents (for schrodinger wave mechanical model)
View Solution
If the three plane $x = y sin ψ + z sin ϕ, y = z sin θ + x sin ψ, z = x sin ϕ + y sin θ,$ intersect in a line, then where $θ, ϕ \in (0, \frac{π}{2})$
$θ, ϕ & ψ$ satisfy
View Solution

The correct Answer is:A

For same n values , distance depends on l value as l value increase distance increases

Similar Questions

Recommended Questions