In three dimension wave function may be expressed in spherical co-ordinate system (r,0,ϕ),r=distance of electron from the nucleus
0= Angle from 'z' axis varying from 0 to π
ϕ= Angle from 'x' axis …… 0 to 2π ltbr> Ψ may be represented as
Ψ(r,0,ϕ)=R(r).A(0,ϕ)
The R(r) is detemind by 'n' and 'l'. The A (0,ϕ) is determined by 'l' and 'm'.
Angular part of 'H' atom wave equation A(0,ϕ)=1√4π.Hence , atomic orbital is:
'dxz'orbital
'px'orbital
'py'orbital
s-orbital
The correct Answer is:d
Step by step video, text & image solution for In three dimension wave function may be expressed in spherical co-ordinate system (r,0,phi),r=distance of electron from the nucleus 0= Angle from 'z' axis varying from 0 to pi phi = Angle from 'x' axis …… 0 to 2pi ltbr. Psi may be represented as Psi (r,0,phi)=R (r) .A(0, phi) The R(r) is detemind by 'n' and 'l'. The A (0,phi) is determined by 'l' and 'm'. Angular part of 'H' atom wave equation A(0,phi)= (1)/sqrt(4pi).Hence , atomic orbital is: by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:Match the column type
Explore 16 Videos
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:Subjective Type
Explore 55 Videos
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:Multiple Objective Type
Explore 49 Videos
- CHEMICAL EQUILIBRIUMBook:GRB PUBLICATIONChapter:CHEMICAL EQUILIBRIUMExercise:D.Le Chateliera principle
Explore 16 Videos
Similar Questions
Knowledge Check
In three dimension wave function may be expressed in spherical co-ordinate system (r,0,ϕ),r=distance of electron from the nucleus
0= Angle from 'z' axis varying from 0 to π
ϕ= Angle from 'x' axis …… 0 to 2π ltbr> Ψ may be represented as
Ψ(r,0,ϕ)=R(r).A(0,ϕ)
The R(r) is detemind by 'n' and 'l'. The A (0,ϕ) is determined by 'l' and 'm'.
Which of the following is R(r) part of '3p' atomic orbital of hydrogen atom [Givenα0=0.529Å]?A2(a0)3/2e−r/a0B227(13a0)3/2(27−18ra0+2ra20)e−r/3a0C2(2a0)3/2(2−ra0)e−r/2a0D181√3(2a0)3/2(6−ra0)e−r/3a0Given wave function represents which orbital of hydrogen Psi=1/4 1/(sqrt2pi)(1/(alpha_(0)))^(5//2) re^(-r//2alpha)cos 0
(where 0=angle from z-axis)A2PyB2PzC3PyD3PZThe wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
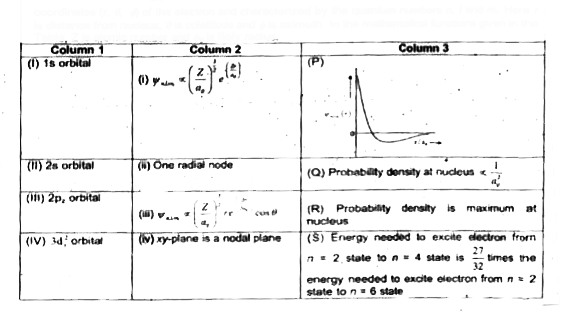
For hydrogen atom, the only correct combination isA(I)(iv)(R)B(I)(i)(P)C(II)(i)(Q)D(I)(i)(S)
If 0<θ,ϕ<π and 8cosθcosϕcos(θ+ϕ)+1=0 find θ and ϕ
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
Which of the following wave function cannot represent an atomic orbital of H-atom?
View SolutionThe wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

For He+ ion the only Incorrect combination is
View SolutionThe second derivative of a single valued function parametrically represented by x=ϕ(t)andy=ψ(t) (where ϕ(t)andψ(t) are different function and ϕ'(t)≠0) is given by
View SolutionFor any real numbers θ and ϕ we define θRϕ if and only if sec2θ−tan2ϕ=1 the relation R is
View Solution

