A particle of mass 4 kg is acted upon by steady force of 4 N.Distance travelled by the particle in 4 sec is
16 m
2 m
8 m
4 m
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Mass of the particle (m) = 4 kg
- Force acting on the particle (F) = 4 N
- Time (t) = 4 seconds
Step 2: Calculate the acceleration using Newton's second law
According to Newton's second law, the force is related to mass and acceleration by the equation:
F=m⋅a
We can rearrange this to find acceleration (a):
a=Fm
Substituting the values:
a=4N4kg=1m/s2
Step 3: Use the equation of motion to find the distance traveled
The equation of motion that relates distance (S), initial velocity (u), acceleration (a), and time (t) is:
S=ut+12at2
Since the particle starts from rest, the initial velocity (u) is 0:
S=0⋅t+12at2
S=12at2
Step 4: Substitute the values into the equation
Now, substituting the values of acceleration and time:
S=12⋅1m/s2⋅(4s)2
S=12⋅1⋅16
S=162=8m
Conclusion
The distance traveled by the particle in 4 seconds is 8 meters.
---
- Mass of the particle (m) = 4 kg
- Force acting on the particle (F) = 4 N
- Time (t) = 4 seconds
According to Newton's second law, the force is related to mass and acceleration by the equation:
F=m⋅a
We can rearrange this to find acceleration (a):
a=Fm
a=4N4kg=1m/s2
The equation of motion that relates distance (S), initial velocity (u), acceleration (a), and time (t) is:
S=ut+12at2
S=0⋅t+12at2
S=12at2
Now, substituting the values of acceleration and time:
S=12⋅1m/s2⋅(4s)2
S=12⋅1⋅16
S=162=8m
The distance traveled by the particle in 4 seconds is 8 meters.
Topper's Solved these Questions
Similar Questions
A force of 2N acts for 5seconds on a particle of mass 0.5kg initially at rest. Calculate the distance moved by the particle in (i) these five seconds and (ii) next 5seconds
View SolutionThe variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is
View Solution
Knowledge Check
A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
Aits displacement will be in simple harmonicBits velocity will be in simple harmonicCits acceleration will be in simple harmonicDNone of the aboveThe variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is
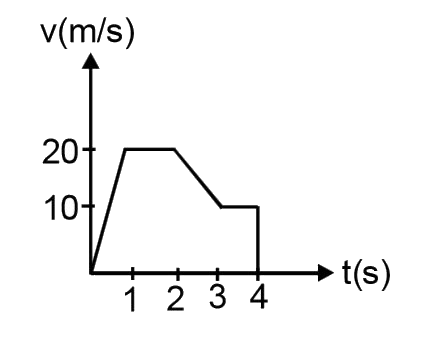 A25mB30mC55mD60m
A25mB30mC55mD60mFrom the adjoining graph, the distance traversed by particle in 4 sec, is-
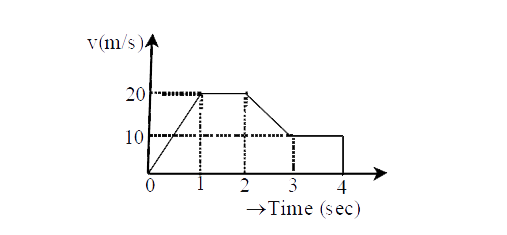 A60 mB25 mC55 mD30 m
A60 mB25 mC55 mD30 m
The variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is?
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionThe motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View Solution