A ball strikes a bat with velocity v. The ball has mass m and after striking it retraces its path. What is the impulse imparted by the bat ?
3 mv
mv
zero
2 mv
To solve the problem of finding the impulse imparted by the bat to the ball, we can follow these steps:
Step 1: Understand the Concept of Impulse
Impulse is defined as the change in momentum of an object. Mathematically, impulse (J) can be expressed as:
J=Δp
where Δp is the change in momentum.
Step 2: Define Initial and Final Momentum
1. Initial Momentum (p_initial): The ball is moving towards the bat with a velocity v. Therefore, the initial momentum of the ball can be calculated as:
pinitial=m⋅v
(where m is the mass of the ball).
2. Final Momentum (p_final): After striking the bat, the ball retraces its path, which means it moves in the opposite direction with the same speed v. Thus, the final momentum of the ball is:
pfinal=m⋅(−v)=−m⋅v
Step 3: Calculate the Change in Momentum
The change in momentum (Δp) can be calculated as:
Δp=pfinal−pinitial
Substituting the values we found:
Δp=(−m⋅v)−(m⋅v)
Δp=−m⋅v−m⋅v
Δp=−2m⋅v
Step 4: Determine the Impulse
Since impulse is equal to the change in momentum, we have:
J=Δp=−2m⋅v
However, impulse is often expressed in terms of magnitude, so we can take the absolute value:
|J|=2m⋅v
Conclusion
The impulse imparted by the bat to the ball is:
J=2m⋅v
Final Answer
The impulse imparted by the bat is 2mv.
---
Impulse is defined as the change in momentum of an object. Mathematically, impulse (J) can be expressed as:
J=Δp
where Δp is the change in momentum.
1. Initial Momentum (p_initial): The ball is moving towards the bat with a velocity v. Therefore, the initial momentum of the ball can be calculated as:
pinitial=m⋅v
(where m is the mass of the ball).
pfinal=m⋅(−v)=−m⋅v
The change in momentum (Δp) can be calculated as:
Δp=pfinal−pinitial
Substituting the values we found:
Δp=(−m⋅v)−(m⋅v)
Δp=−m⋅v−m⋅v
Δp=−2m⋅v
Since impulse is equal to the change in momentum, we have:
J=Δp=−2m⋅v
However, impulse is often expressed in terms of magnitude, so we can take the absolute value:
|J|=2m⋅v
The impulse imparted by the bat to the ball is:
J=2m⋅v
The impulse imparted by the bat is 2mv.
Topper's Solved these Questions
Similar Questions
A ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?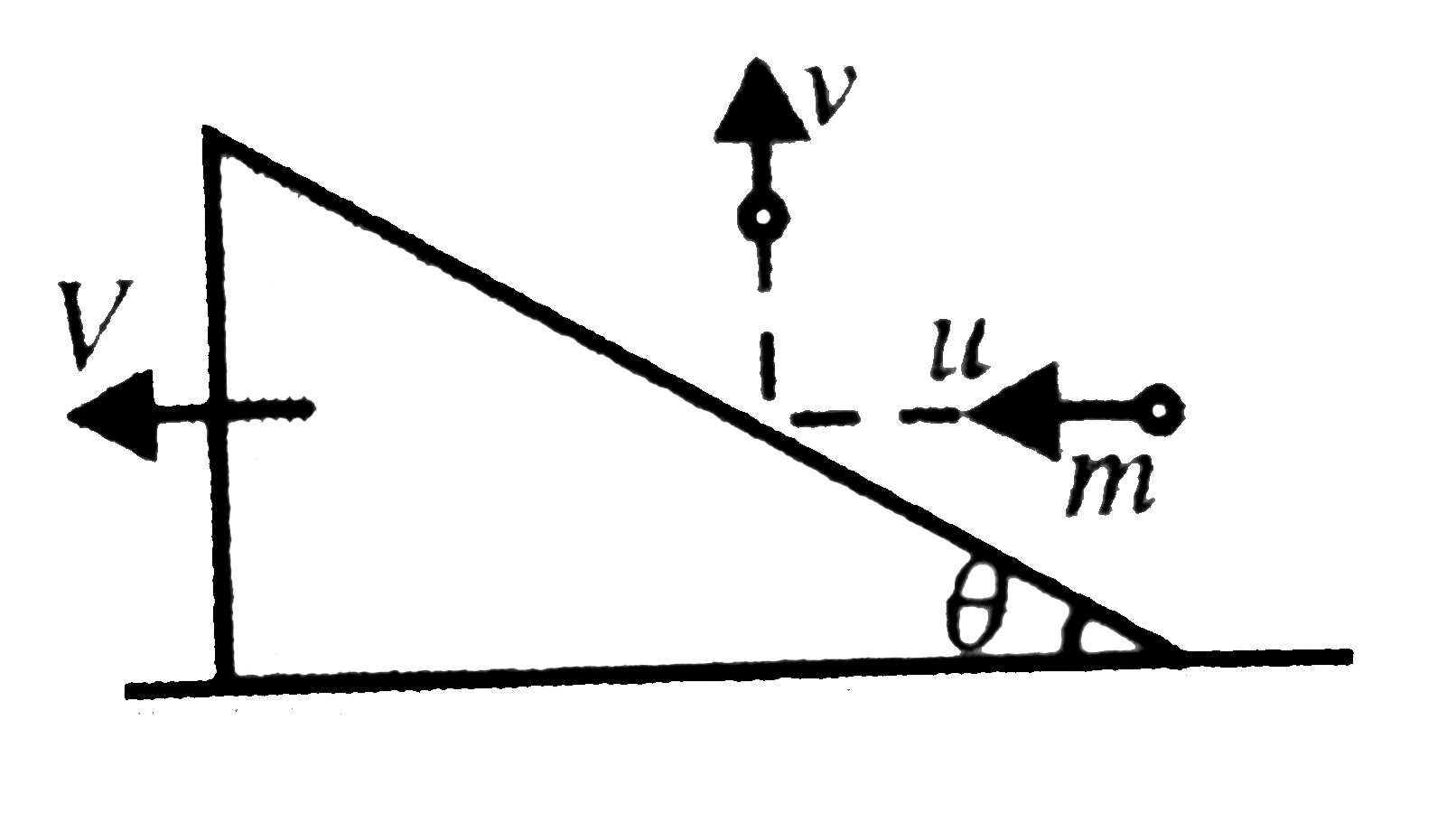
View SolutionA ball is projected with velocity v0 at an angle α to the horizonal, towards a smooth wall which appraches the ball. With velocity u. After collision the ball retraces its path to the point of projection . What is the time t taken by the ball form the instant of projection to point of impact ?

View Solution
Knowledge Check
A cricket ball of mass 150g is moving with a velocity of 12 m/s and is hit by a bat so that the ball is turned back with a velocity ishit by a bat so that the ball is turned back with a velocity of 20 m/s. The force of blow acts for 0.01 s on the ball. What is the averate force exerted by the bat on the ball?
A240NB300NC380ND480NA ball of mass m is moving towards a batsman at a speed v. The batsman strikes the ball and deflects it by an angle θ without changing its speed. The impulse imparted to the ball is given by
AmvcosθBmvsinθC2mvcos(θ2)D2mvsin(θ2)STATEMENT - 1 : A ball of mass m is moving towards a batsman at a speed v. The batsman strikes the ball and deflects it by an angle θ without changing its speed. The impulse imparted to the ball is zero.
because
STATEMENT - 2 : Impulse = change in momentum.AStatement - 1 is True, Statement - 2 is True, Statement - 2 is a correct explanation for Statement - 1.BStatement - 1 is True, Statement - 2 is True, Statement - 2 is NOT a correct explanation for statement - 1.CStatement - 1 is True, Statement - 2 is False.DStatement - 1 is False, Statement - 2 is True.
A cricket ball of mass 100g has initial velocity →u=(3ˆi+4ˆj)ms and final velocity →v=(−3ˆi−4ˆj)ms after being hit by the bat.The magnitude of the impulse on the bat by the ball will be
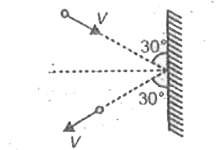
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionA ball of mass 1kg strink a heavy platform, elastically, moving upwards with a velocity of 5m/s. The speed of the ball just begore the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is :-
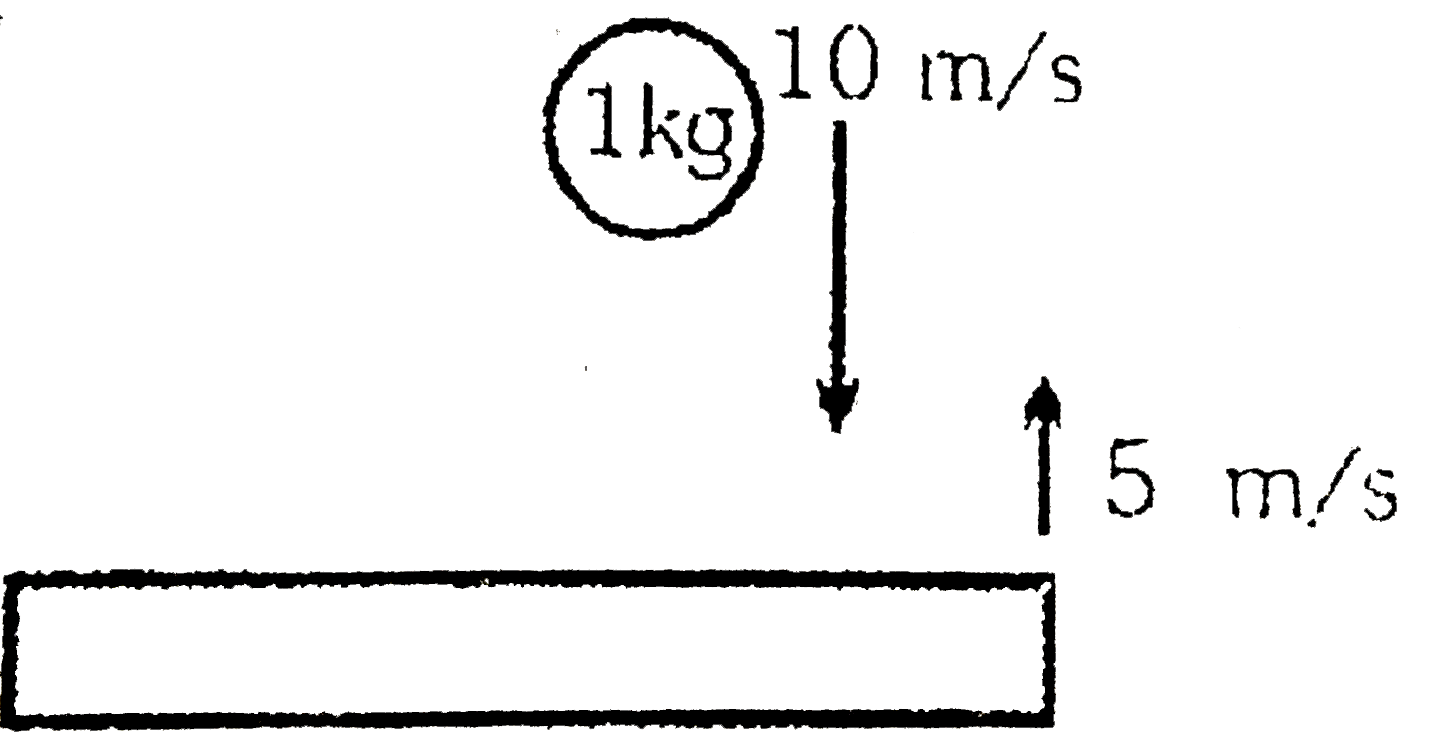
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is

View Solution
