A ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle. Calculate the change in momentum.
To solve the problem of calculating the change in momentum of a ball striking a wall at an angle of 45∘ and being reflected at the same angle, we can follow these steps:
Step 1: Understand the Initial Momentum
The initial momentum of the ball is given as Pi=5kg m/s.
Step 2: Analyze the Collision
The ball strikes the wall at an angle of 45∘ and is reflected at the same angle. This means that the angle of incidence is equal to the angle of reflection.
Step 3: Resolve the Initial Momentum into Components
We need to resolve the initial momentum into its x and y components:
- The x-component of the initial momentum (Pix) can be calculated using:
Pix=Picos(45∘)=5⋅1√2=5√2kg m/s
- The y-component of the initial momentum (Piy) can be calculated using:
Piy=Pisin(45∘)=5⋅1√2=5√2kg m/s
Step 4: Resolve the Final Momentum into Components
After the collision, the ball is reflected at the same angle, so the components of the final momentum will be:
- The x-component of the final momentum (Pfx):
Pfx=−Picos(45∘)=−5√2kg m/s
- The y-component of the final momentum (Pfy):
Pfy=Pisin(45∘)=5√2kg m/s
Step 5: Calculate the Change in Momentum
Now, we calculate the change in momentum for both the x and y components:
- Change in x-momentum (ΔPx):
ΔPx=Pfx−Pix=−5√2−5√2=−10√2kg m/s
- Change in y-momentum (ΔPy):
ΔPy=Pfy−Piy=5√2−5√2=0kg m/s
Step 6: Final Result
The total change in momentum is primarily in the x-direction:
ΔP=√(ΔPx)2+(ΔPy)2=
⎷(−10√2)2+02=10√2kg m/s
Conclusion
The change in momentum of the ball is:
ΔP=10√2kg m/s≈7.07kg m/s
This change occurs in the x-direction.
---
The initial momentum of the ball is given as Pi=5kg m/s.
The ball strikes the wall at an angle of 45∘ and is reflected at the same angle. This means that the angle of incidence is equal to the angle of reflection.
We need to resolve the initial momentum into its x and y components:
- The x-component of the initial momentum (Pix) can be calculated using:
Pix=Picos(45∘)=5⋅1√2=5√2kg m/s
- The y-component of the initial momentum (Piy) can be calculated using:
Piy=Pisin(45∘)=5⋅1√2=5√2kg m/s
After the collision, the ball is reflected at the same angle, so the components of the final momentum will be:
- The x-component of the final momentum (Pfx):
Pfx=−Picos(45∘)=−5√2kg m/s
- The y-component of the final momentum (Pfy):
Pfy=Pisin(45∘)=5√2kg m/s
Now, we calculate the change in momentum for both the x and y components:
- Change in x-momentum (ΔPx):
ΔPx=Pfx−Pix=−5√2−5√2=−10√2kg m/s
- Change in y-momentum (ΔPy):
ΔPy=Pfy−Piy=5√2−5√2=0kg m/s
The total change in momentum is primarily in the x-direction:
ΔP=√(ΔPx)2+(ΔPy)2=
⎷(−10√2)2+02=10√2kg m/s
The change in momentum of the ball is:
ΔP=10√2kg m/s≈7.07kg m/s
This change occurs in the x-direction.
Topper's Solved these Questions
Similar Questions
A ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle Calculate the impulse .
View SolutionA ball moving with a momen - tum of 15kgms−1 strickes against the wall at an angle of 30∘ and is reflected back with the same momentum at the same angle . Calculte impulse.
View Solution
Knowledge Check
A ball moving with a momemtum 5 kg ms−1 strikes a wall. If the initial and final momenta make equal angles of 45∘, then magnitude in change in momentum is
A5.05 kg ms−1B7.07 kg ms−1C10.00 kg ms−1D0 kg ms−1A 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
A96 NB48 NC24 ND40 NA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96N
A 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
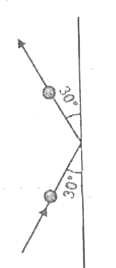
View SolutionA tennis ball of mass 'in' strikes the massive wall with vel V and traces the same path. Calculate the change in momentum.
View SolutionAn object of m kg with speed of ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
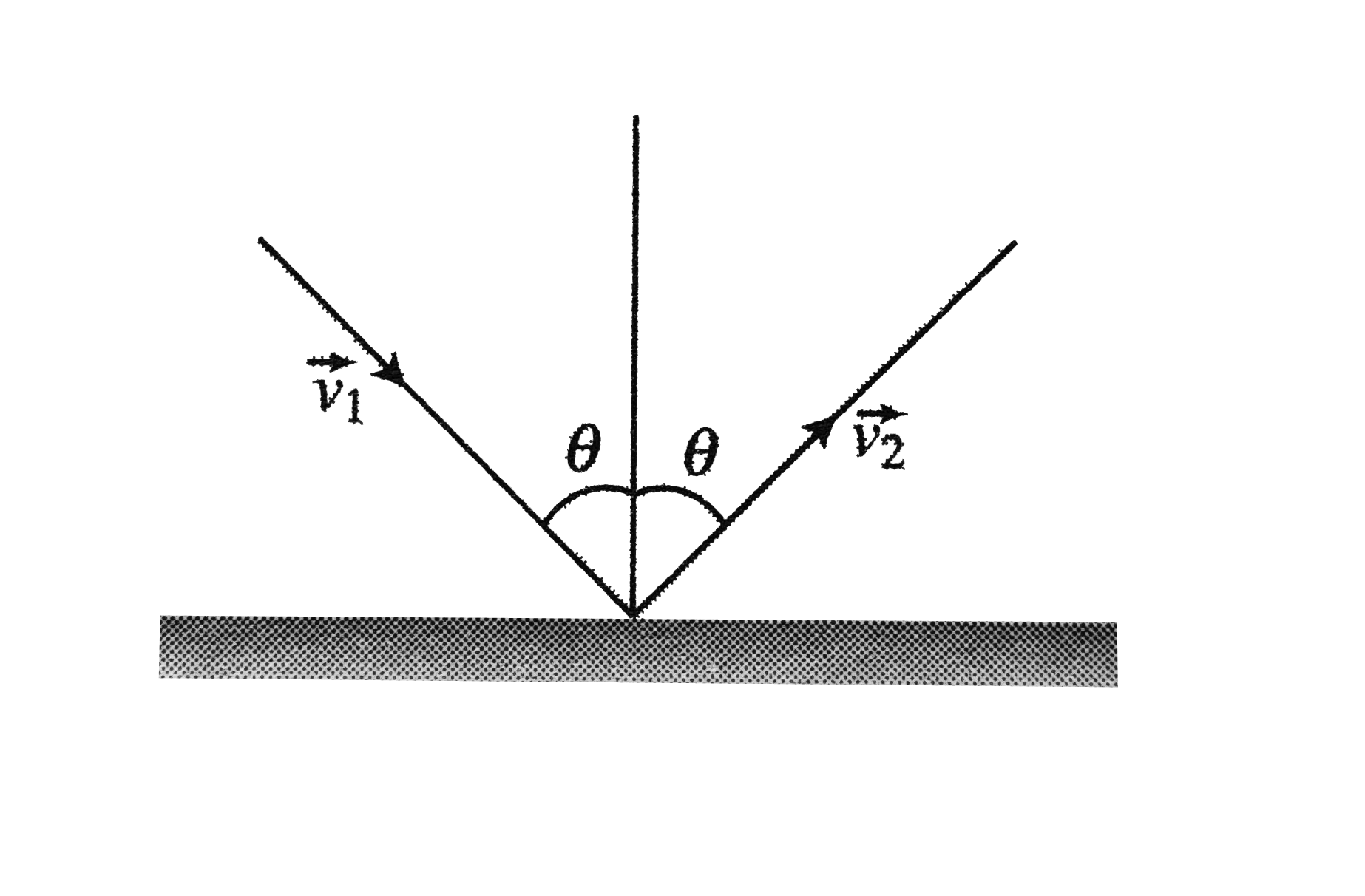
View SolutionThe average force imparted on the wall when a 0.75 kg ball moving with a speed of 18 m/s strikes it at an angle of 60' for a contact time of 0.15 s and gets reflected with the same speed and at the same angle is P newtons. Then, the value of P/10 is: (Take √3=1.73 )
View SolutionA body of mass 3kg moving with speed 5ms−1 , hits a wall at an angle of 60∘ and return at the same angle. The impact time was 0.2 sec. calculate the force exerted on the wall :
View Solution

